Assignment 4

Assignment 4 (75 points, Due Mon. October 12)
Reading

Bix, Ch 1, Sec 1, pp. 21-37

Bix, Ch 1, Sec 0, pp. 4-15 (review: compare with B&B)

GTC, Chapters 3 and 4

Main ideas

Signed distances and ratios

Thales Theorem extended to signed ratios(cf. Bix theorems 1.11 and 1.12)

Distances, perpendicular bisectors and circumcircles from GTC. Be able to explain the "two-ripple" and "three-ripple" figures.

Chords and inscribed polygons from GTC, Chapter 3.

Right triangle properties and Carpenter

Application of Carpenter to constructions and to problems.

Problems to Turn In

In these proofs you can use theorems in B&B, Chaps 1-4 and the reading in GTC and Bix.

You may find that Sketchpad is very helpful in investigating problems.

4.1 Concurrence of Perpendicular Bisectors (10 points)

B&B p. 255 #18 (previously assigned as 2.6)

Draw an obtuse triangle and also a right triangle. With straightedge and compass, construct the circumcircle of each triangle. Where is the circumcenter in each case?

4.2 Parallelograms (30 points)

Prove the following problems on B&B, pp 113-114. Important: Use the definition of a parallelogram at the beginning of the Exercises on p. 113. Do not use other equivalent definitions.

For tools, you can use anything proved in B&B through p. 122.

Prove 2 and its converse 5.
Prove 3 and its converse 7.
Prove 4 and its converse 8.
Prove 6.

4.3 Rhombi (15 Points)

(a) A rhombus is defined to be a quadrilateral with four equal sides. Prove that a rhombus is a parallelogram.

(b) Prove that a parallelogram with perpendicular diagonals is a rhombus.

4.4 Three transversals (10 Points)

BB p. 127 #4

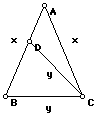
4.5 A special triangle (10 Points)

Let ABC be an isosceles triangle (AB=AC) and let D be a point on segment AB so that CD = CB.

(a) What is the relationship among the lengths AB, BC and DC?

(b) If triangle DAC is also isosceles (i.e., DA=DC), what can you conclude about ABC?

Constructions (to do but not turn in)

Be prepared to construct

(a) A line segment 4/7 the length of a given segment.

(b) A line segment (1+a) times the length of a given segment, where a is the square root of 5.

Given a point P exterior to a circle, construct the tangent lines to the circle through P.

Return to Math 444 Home Page