Read about SSS, SAS, ASA congruence criteria

Look over the whole chapter. Skip the "real-world applications" to family disputes but do pay attention to the sections on geometry, pp. 12-36. You should understand the role of undefined terms, axioms, "if-then" statements and their converses, "if and only if" statements, "begging the question" and the role of diagrams, good and bad.

(Some of this will be done in class Monday, as much as time permits; it may be checked in class on Wednesday.)

In these proofs you can use the triangle congruence criteria, SAS, SSS, ASA and the basic properties of isosceles triangles stated in Theorems A, B, C of B&B, p. 20-23.

If a quadrilateral ABCD has AB = DA and BC = CD, we call this quadrilateral a kite. (Compare B&B, page 24, problems #2 and #3, but notice the difference in labeling the vertices.)

(a) State and prove a proposition about a relationship between angles of such a kite.

(b) State and prove a proposition about a relationship between the diagonal lines, line AC and line BD, of such a kite.

Caution: Does your diagram include all cases?

Prove this statement:

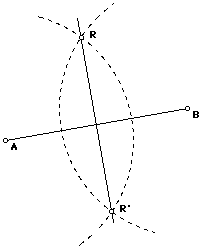
Given a line segment AB, construct two circles of the same radius, with centers A and B. If the two circles intersect at point R and R', then line RR' is the perpendicular bisector of segment AB.

Comment: Include an explicit statement of the definition of a perpendicular bisector in your proof.

Sign up for the class email list, using the instructions given in class and on the web site. Then send an email to the list, giving a brief self-introduction. You may want to include a phone number so classmates can call you.