Contents: Three Proofs | Comments: Another Case | Possible Mistakes | Use to Prove SSS
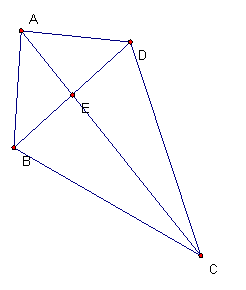
Given ABCD a kite, with AB = AD and CB = CD, the following things are true.

Two statements are in bold type, because those statements include the others, from the definitions or perpendicular bisector and congruence of triangles. (Of course to prove the bold statements, one may have to prove some of the others first.
In class, students were asked to prove this:
Given a kite ABCD with AB = AD and CB = CD, then triangle ABC is congruent to triangle ADC.
Here are two proofs that were found in class (my wording).† (Note: this is an example that shows there is not necessarily just one good proof of a geometrical theorem.)
Proof 1: †(key idea: show angle BAC = angle DAC)
QED (almost Ė see comments below about another case).
Proof 2: (key idea: show angle BAC = angle DAC)
QED (almost Ė see comments below about another case).
Proof 3: (key idea: show angle ABC = angle ADC)
QED (almost Ė see comments below about another case).
Each of the proofs is good, and valid for the figure shown at the top of the page.† However there is another figure that shows another case of a kite, for which the proofs are almost right, but need some additional comments.† This is this case where A and C are both on the same side of line BD, such as in this figure.
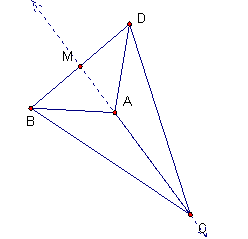
So what goes wrong with the proofs?†
In Proof 1 and Proof 2, an important step was
But this is not true in this figure.† But all is not lost.† We just have to justify angle BAC = angle DAC in this case also. Then the proofs are correct for the remaining steps. We can actually establish and angle equality a couple of ways.
In Proof 3, the step that are not true in this care are
But what if we subtract instead of add, then we still get correct statements that can be used in the rest of the proof.
While there are a number of correct ways to prove the theorem above, there are also a number of erroneous approaches.† Typically, these include a disguised way of assuming the conclusion.† Here are some examples of beginnings of such proofs that triangle ABC is congruent to triangle ADC
|
Problematic Start |
The problem |
|
Let AC and BD intersect at E, then E is the midpoint of BD. |
You canít say E is the midpoint without giving a reason.† |
|
Let M be the midpoint of BD, then let k be the line containing AMB, then by the theory of isosceles triangles, this line bisects angle BAC. |
This has the germ of the right idea, but you can never construct a line through 3 points without explaining why the points are collinear. |
|
Let AC be the perpendicular bisector of BD, †Ö † |
Again, assuming that A and C are on the perpendicular bisector. |
Of course all these facts are true, but at the outset we are trying to prove the basic relations, so we canít assume them to prove them.