Math 487 Lab 10 (Fermat Point)

More relationships from the Napoleon Figure

Make another Napoleon figure (or duplicate an earlier page with this figure) We will explore the consequences of one of the problems in Assignment 9.

Part 1: Relationship between AA' and BB'

• Draw segment AA'
• Rotate AA' to segment B'B.  To do this, you will need to find a center to mark and choose an angle that will do the job.  It should be clear from your choice that the rotation actually does rotate AA' to B'B.

What is the center?  ______________ .What is the angle? ____________

• Now construct the interior of triangle ACA' and rotate this triangle by the same rotation. From this you will have two congruent triangles and thus two sets of equal angles. What angles in the image triangles are equal to these?

  Angle ACA' = ________.  Angle CA'A = _______.  Angle A'AC = _________

• Let point P be the intersection of line AA' and line BB'.  Based on the rotated triangle information above, tell an angle that is equal to each of these.

  Angle A'PC = ________.  Angle PAC = _______. 

Part 2: Enter the circumcircles

• Drag A and B so segments AA' and BB' intersect (not just the lines intersect). 
• Construct the circle with center X through A' (circumcircle of BCA'). How does P appear to be related to this circle? 
• How does the equality of angle PA'C and PBC prove that P is on the circle (think inscribed angles)?

Answer __________________________

• Construct the circle with center Z through C' (circumcircle of ABC'). Explain why P is on this circle.

Answer __________________________

• Construct the circle with center Y through B'(circumcircle of ACB'). How is P related to this circle?  In this case, how do you know the vertex angle P in the quadrilateral AB'CP? How does the value of an angle prove this relationship?

Answer __________________________

·        Another case.  Check that if you drag B so that angle ABC > 120 degrees, the circles still are all concurrent at P, but P now lies outside triangle ABC.

Conclusion:  We have seen that P is on all three circles, so the 3 circumcircles are all concurrent at the point of intersection of AA' and BB'.

Part 3:  Relationships among all 3 segments AA', BB', CC'

• Now draw segment CC'. 
• Can you argue that if AA' meets CC' at point Q, that Q must really be P? (Use the circles.)  Conclude that the lines AA', BB', CC' are concurrent at P.
• How are the segment lengths AA', BB', CC' related?
• What are the angles that the 3 lines AA', BB' and CC' make at P? 

The Fermat Point

The Point P is called the Fermat Point of triangle ABC. 

If the angles of ABC are all less than 120 degrees, P lies inside the triangle.  The rays PA, PB, PC all form equal angles of 120 degrees, as we have seen.  This implies that P is the point inside the triangle for which the sum of distances PA + PB + PC is a minimum.  [We are not proving this yet.]  See http://faculty.evansville.edu/ck6/tcenters/class/fermat.html for some historical background.

Distance and the Fermat point

Continue with a copy of the same page. Hide the 3 segments AA' etc and the triangle interiors, so that the figure looks like the one at the top of the page, with also the Fermat point labeled F.

• Move A, B, C so that F is inside ABC. Measure angles AFB, BFC, CFA. You should get 120 degrees for each.
• Draw a point Q inside triangle ABC and construct segments AQ, BQ, CQ.
• Measure the lengths of these segments and add the 3 lengths AQ + BQ + CQ with the GSP calculator.
• Experiment moving Q around to find the smallest sum of the 3 lengths that you can. Where does this seem to be?

Here is a proof

• Rotate Q by 60 degrees with center A to get Q'. What kind of triangle is AWW'?
• Also construct the interior of triangle AQB and rotate it by the same rotation. Note that B is mapped to C', so angle AQ'C' = angle AQB..

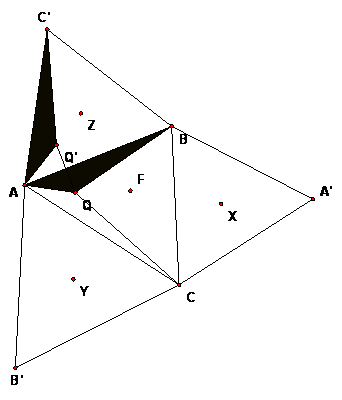
• Then the sum of the distances that we have been studying is equal to the sum CQ + QQ' + Q'C'. Do you see why?
• Therefore, the distance sum is always greater than CC' unless the points Q and Q' are on segment CC'.
• But if this happens, what can you say about angle AQC and angle AQ'C' (= angle AQB), recalling that the angles of triangle AQQ' are all 60 degrees?
• Does this explain why the distance sum is the smallest when Q is exactly = F?