Assignment 3 (Due Wednesday, 10/12)

3.1 Tangent circles

1. Given an angle ABC, prove that a circle is tangent to rays BA and BC if and only if the center P of the circle is on the angle bisector of ABC.
2. Prove that the bisectors of the interior angles of any triangle ABC are concurrent.
3. Prove that for any triangle there is exactly one circle inscribed in the triangle.

3.2 Distance locus for intersecting lines

1. If the distance from a point P to a line m is defined as the distance from point P to the closest point Q on the line, tell how to find this closest point and prove that this is the correct point.
2. Given two intersecttng lines, tell what is the set of points equidistant from each line and prove your assertion.

3.3 Inscribed circles

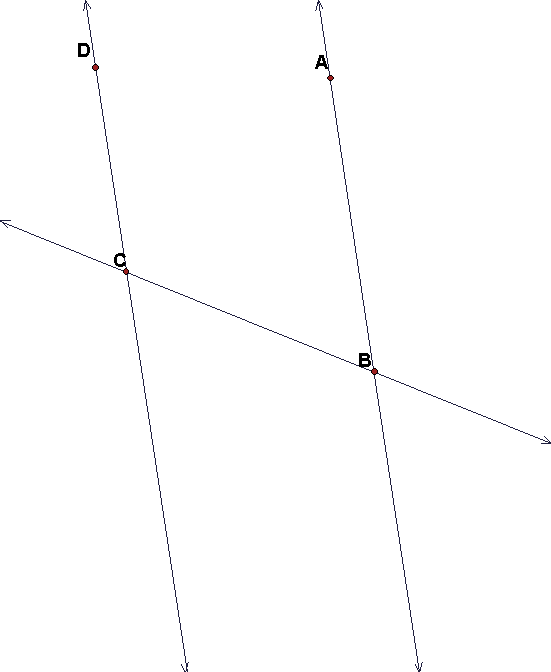
1. The lines AB and CD may be parallel.  In any event any point of intersection if far off this page. Construct all circles tangent to all 3 lines in the figure. You can draw your own figure more or less like this for your construction.
2. Explain carefully the steps of your construction and tell clearly why it works.

3.4 Angle sum of a polygon

1. For a convex n-sided polygon, what is the sum of the interior angles?
2. Prove your statement above.
3. For a convex n-sided polygon, what is the sum of the exterior angles?
4. Prove your statement above.
5. Is this formula still true for a nonconvex quadrilateral? Justify your answer..