Definition: A golden rectangle is a rectangle that can be cut up into a square and a rectangle similar to the original one. More precisely,
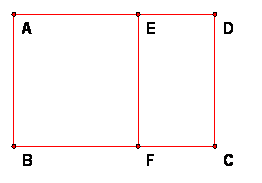
Let ABCD be a rectangle, with width AB < length BC. Then there is a point E on segment AD and a point F on segment BC so that BFEA is a square. i.e., AE = BF = AB (and consequently EF = AB also). Then FCDE is a rectangle. We say that ABCD is a golden rectangle if FCDE is similar to ABCD.

Theorem: All golden rectangles are similar and the ratio length/width = golden ratio = (1+ sqrt 5)/2.
Corollary. If ABCD is a golden rectangle, so is the sub - rectangle FCDE (as defined above).
Proof: Let a = AB = width and b = BC = length of a golden rectangle. Then for ABCD the ratio length/width = b/a and for FCDE the ratio length/width = a/(b-a). The rectangles are similar if and only if these ratios are equal, so, if we set k = b/a, then b = ka and k = b/a = a/(b-a) = a/(ka – a) = 1/(k-1).
Therefore k is a root of k^2 – k – 1 = 0; also, k is a positive number. By the quadratic formula the only positive root of this polynomial is the golden ratio (1+ sqrt 5)/2.
QED
|
The golden ratio, as we have seen also appears many times in the regular pentagon and its pentagram of diagonals. This figure shows a square and two golden rectangles attached to this pentagon figure. |
|
Since the sub-rectangle FDCE can also be divided into a square and a still smaller golden rectangle, one can continue this process to get an infinite number of smaller and smaller squares spiraling inside the original golden rectangle.
For a figure showing this, go to this link at Mathworld or to this link at UBC
or this link at the BBC.