Parallelograms in the coordinate plane

Construct a figure like this one with Sketchpad using the following steps.

In the graph menu,

• Choose Define New Parameter, and make the parameter 1 cm. Don't forget the unit!
• With the parameter selected on the screen, choose Define Unit Distance.
• Also, check the item Snap Points.

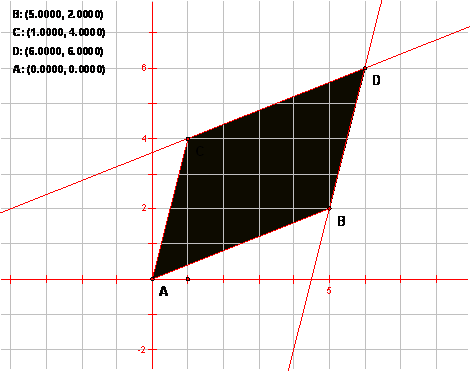
Then, letting A be the origin, draw segments AB and AC. Construct a parallelogram ABDC.

• Select all 4 points and choose Measure > Coordinates. If the points have snapped properly, then the coordinates should all be integers.

• Write down the coordinates of the points A, B, C, D.

• Also, measure the equation of line CD.

Now let E be the intersection of the y-axis and the line CD (i.e., the y-intercept). Construct point F so that ABFE is a parallelogram.

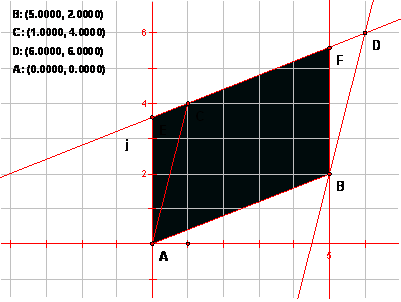
• Measure the areas of ABDC and ABFE. How do they compare. Why?

• Using the segment AE as the base, what are the measures of the base and height of ABFE?

Getting a Formula

Now follow this same construction process but this time instead of numbers, use letters for the coordinates. Let B = (a,b) and C = (c, d).

• Find the equation of line CD and the coordinates of E.
• Then compute the base and height of ABFE and find the area.
• Then tell how this area compares with the original area of ABDC.

You should have a formula for the area of the parallelogram ABDC without doing a gruesome calculation involving the height of ABDC because you found the area of a simpler parallelogram with the same area. You may find the expression in the formula looks familiar from another course.