Orbits of Transformations

The concept of an orbit is a key one in transformational geometry. Later on this page will be a general definition of orbit, but we begin by explaining the simplest case: the orbit of a single transformation of the plane.

Powers of a transformation

Recall that for a transformation, the power T¹ = T and T² means TT, or T composed with T.  Likewise, for positive integers k, T^k = TT^k-1 is the composition T…T, where T is written k times.  Then the usual exponential law is clear for positive integers:  T^mTⁿ = T^m+n. 

As with exponential notation for numbers, it makes sense to extend this notation to T⁰ = I = identity transformation.  Since SI = IS = S for any transformation S, it is true that T^mT⁰ = T^m+0 = T^m.  Also, writing the inverse of T as usual as T^-1, it is true that T¹T^-1 = T⁰ = I.  If for a positive integer k, we write T^-k for (T^-1)^k, this gives a consistent way of writing Tⁿ for any integer, positive or zero or negative, so that 

T^mTⁿ = T^m+n. 

Orbits of a Single Transformation

Definition: Suppose T is a transformation of the plane and P is a point of the plane. 

• The forward T-orbit of P is the set of all the points P, T(P), T²(P), … T^k(P), … for all non-negative k. Note: P = T⁰(P).
• The (full) T-orbit of P is the set of all the points P, T(P), T²(P), … T^k(P), … for all integers k, including negative ones and k = 0.

Some examples will help visualize this concept.

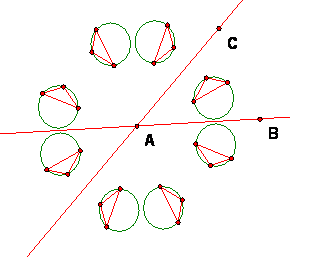
Example 1: Orbit by a Rotation of 72 degrees with center O If T is rotation by angle 72 degrees with center O, then for any P not equal to O, the orbit is a set of 5 points that are the vertices of a regular pentagon.  The orbit is a finite set of points because in this case, T5 = T0 = I, so the only powers of T that are distinct are Tk, k = 0, 1, 2, 3, 4.  Notice that T-1 = T4, so the forward orbit and the full orbit are the same. If Q is another such point, the orbits of P and Q are different sets, unless it happens that Q = Tk(P) for some k, so that Q is one of the points in the orbit of P.

Note: the orbit of point O is a special case.  For rotation by any angle a, the orbit of O consists of the one point O.

In general, for P distinct from O, for a rotation with center O and angle a, the orbit is a finite set of points if a is a rational number in degree measure (or a rational multiple of 2pi in radian measure).  This true because for such rotations, if a = (p/q)*360, T^q = I.

On the other hand, if the angle is an irrational multiple of 360 degrees (or 2 pi radians), all the points T^k(P) are distinct and the orbit is infinite (also the forward and the full orbit are not the same).

Example 2:  Orbit by a translation

Suppose that T is translation by vector AB, where A and B are distinct points.  If P is a point, then the forward T-orbit of P is an infinite row of equally-spaced points on a ray with origin P.

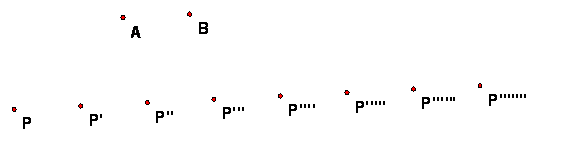
The full T-orbit of P is a row of equally spaced points on a line through P, going to infinity in both directions.

Example 3:  Orbit of a line reflection

Suppose T is reflection in a line m.  If P is any point, let P' = T(P).  Then P = T(P') by definition of line reflection.  So there are two kinds of T-orbits.

• If P is not on m, then the orbit of P consists of two points:  P and P'.
• If P is on m, then the orbit of P consists of one point:  P (since P' = P).

In both cases the forward orbit and the full orbit are the same.

Example 4:  Orbit of a point reflection

If T is a point reflection with center O, then for any P, let P' be the point reflection of P with respect to O. 

• If P is distinct from O, the (forward or full) T-orbit of P consists of two points:  P and P'.
• If P = O, then the orbit of P consists of one point:  P (since P' = P).

This can be seen in the same way as the line reflection orbit.  But it can also be considered as a rotation orbit, by a rotation of 180 degrees.

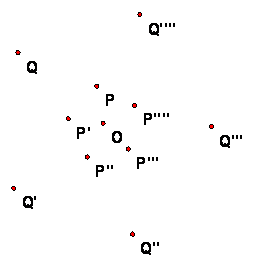
Example 5:  Spiral orbit of a rotary dilation

A transformation need not be an isometry to have an orbit.  For example, suppose that T is a transformation that is the composition of a rotation with center O (by a non-zero angle) composed with a dilation with center O and scaling ratio r > 1.  Then the orbit of a point P distinct from O will consist of an infinite set of points on a spiral as in this figure.

Orbits of sets by a single Transformation

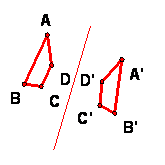
The definition of the orbit of a set of points can be extended to a definition of the orbit of a plane figure, such as a quadrilateral ABCD, or some other set of points.  This orbit is simply the set of points in the orbits of all the points in the figure. Of course the orbit of any single point in the figure is a subset of the orbit of the whole figure.

For example, the orbit of the quadrilateral ABCD, when T is line reflection, is a figure consisting of two congruent quadrilaterals:

This example shows part of the forward T-orbit of a triangle PQR by a translation T.

This shows an orbit of PQR by a translation by a different vector:

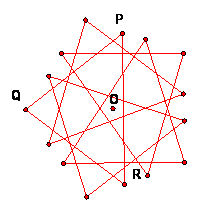
Finally, here are two examples of orbits of triangles PQR by a rotation of 72 degrees, with center O.  Notice that the orbit of any individual point, such as P, still consists of the vertices of a regular pentagon.

 

Orbits by Two Transformations

Suppose that U and V are transformations of the plane, and P is a point. 

• The forward {U,V}-orbit of P is the set of points of the form Z(P), where Z is a product of non-negative integer powers of U and V (e.g, Z = UV, or VU, or V⁴U³V).  In other words, start with P and construct as many points as possible by transforming P by U and by V, then transforming the two images each by U and V, then transforming those images, and so forth.
• The (full) {U,V}-orbit of P is defined almost the same way, as the set of points of the form Z(P), where Z is a product of integer powers (positive, negative or zero) of U and V (e.g, Z = UV^-1, or V^-1U^-2V^-1, or V^-4U³V).  In other words, start with P and construct as many points as possible by transforming P by U and by V or their inverses, then transforming the two images each by U and V, or their inverses, then transforming those images, and so forth.
• The {U,V}-orbit of a figure, or set of points can be defined as before, as the set of points in the orbits if the points in the figure.

Examples of orbits by two transformations are much more interesting and complex than those by one transformation.  Some of these examples will be the subject of labs and problems.  Here are a few examples.

Example 6:  Orbit of a point by two translations

Let ABC be a triangle and let S be translation by AB and T be translation by BC.   In lab 8, the {S,T} orbit of a point P was constructed; it was a lattice. (The point P in the lab was actually point A.)  This is an infinite set.  (We only draw the points in a finite region of the plane, of course)

Specifically, the forward orbit is a quadrant of a lattice, consisting of translations of the point P by vectors mAB + n AC, where m and n are nonnegative integers.

The full orbit can be constructed by translating images also by vectors BA = -AB and CA = -AC as well as AB and AC.

Example 7: Orbit of a polygon by two line reflections

This example was explored with Sketchpad in a kaleidoscope experiment in Lab 2 (part B).  In this case, there were two lines meeting at a 45-degree angle.  Then U was reflection in one line and V reflection in the other.  Then for some figure F, reflect F by U then by V and over and over.  In this case, there are only a finite number (eight or fewer) of distinct images of F.  All the other images coincide with one of these.  Also the forward orbit is the full orbit (which is not surprising, since U^-1 = U; all powers of U and V can be written with positive exponents). 

Here is an example of the orbit of a figure consisting of a triangle inscribed in a circle.  Notice the eight congruent figures.  Both lines AB and AC are lines of symmetry of this figure.  Reflecting in either one does not create any new figures.