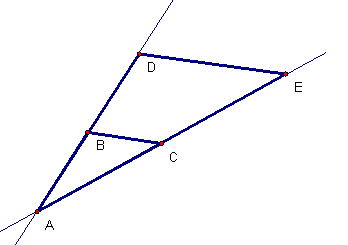
After introducing the Dilation Axiom, we studied several “Thales figures” of similar triangles like ABC and ADE here. The triangles have a shared angle BAC = angle DAE and sides that are proportional: AD/AD = AE/AC. This is a special case of SAS similarity. We can think of these triangles as “nested.” Not only are all the corresponding angles congruent and the corresponding sides proportional, but we have learned that line DE is parallel to line BC.

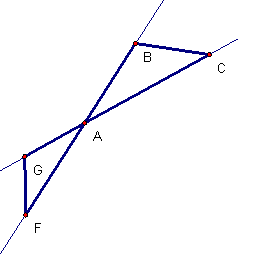
However, there are other ways for similar triangles to share an angle. Imagine reflecting triangle ADE in the angle bisector of angle BAC. Then the reflected triangle would look like the new triangle below. In this figure, triangle ADE (above) is congruent to triangle AGF (below), so triangle AGF is similar to triangle ABC. We can think of these triangles as “nested but twisted”. Line FG is never parallel to line BC, except in the isosceles case where AB = AC.
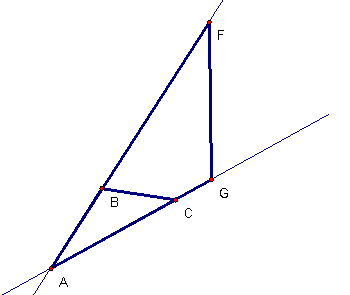
In this figure the two triangles clearly have one angle the same. But the correspondence of vertices adn thus the correspondence of sides is different.
What vertices in the second triangle correspond to vertices B and C in triangle ABC? _________
What equality of ratios must be true for triangle ABC to be similar to triangle AGF by SAS? _____
We can think of this figure as a “reflected Thales” figure.
In other examples, the figure may be a little harder to analyze because of overlaps, but the relationship is exactly the same, so just draw a separate picture of each triangle and figure out the corresponding vertices and what the ratio must be for SAS.
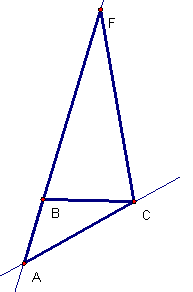
Here are a couple of examples. In the first, side BC intersects FG. In the second, the vertex G actually is the same point as C, so we have triangle ABC is similar to triangle ACF.
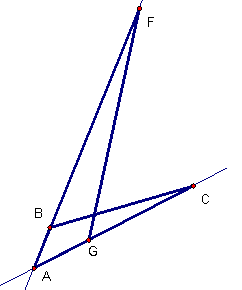
A final pair of figures shows what happens if two triangles share a pair of vertical angles. Again, there are two ways that the equal angles and the vertices can correspond to give similarity by SAS. Again there are two kinds of figures, one with parallel corresponding sides and the other not.
In each case, what is the equality of ratios that will show these triangles are similar by SAS?
Figure on the left _______________ Figure on the right ____________________