Triple Line Reflection and Glide Reflections

Let u, v, w be 3 lines in the plane. This has already been proved.

Theorem 1

If u, v, w are either concurrent or parallel, then the composition of the 3 line reflections R_wR_vR_u is a line reflection.

This theorem will now be proved.

Theorem 2

If u, v, w are not concurrent or parallel, then the composition of the 3 line reflections R_wR_vR_u is a glide reflection.

The proof will break down into several steps.

1. The composition of a half turn H_A and a line reflection R_m is a glide reflection when center A is not on mirror line m and a line reflection when A is on m.
2. The composition of any rotation A_x and a line reflection R_m is a glide reflection when center A is not on mirror line m and a line reflection when A is on m.
3. Theorem. 2 follows from the previous step.

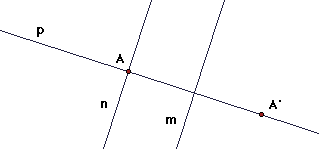
Step 1. Let H be the half turn with center A and let R be line reflection in m. We will prove that RH is the glide reflection G_AA' where A' = R(A).

Then define p as the line through A perpendicular to m and n as the line through A perpendicular to p (and thus parallel to m).

It is known from the theorem on double line reflections, that for any two lines c and d perpendicular at A, the half-turn H = R_c R_d, since the rotation angle = 2*90 degrees. So in particular H = R_n R_p. H also equals R_p R_n.

But then RH = R(R_nR_p ) = (RR_n)R_p. Since m and n are parallel and perpendicular to p, RR_n is a translation parallel to p. Since R(R_n(A)) = R(A) = A', the translation vector is AA' and RR_n = T_AA'. This is the identity when A = A' (when A is on m) and a translation by a non-zero vector (when A is not on m).

But then RH = T_AA'R_p and this is precisely the definition of the glide reflection

G_AA'. (Except that RH = R_p is a line reflection if A is on m.)

Also, the isometry HR is the inverse of RH, since (HR)(RH) = H(RR)H = HH = I. But this means HR = G_A'A is also a glide reflection.

Step 2. Prove that for any rotation S with center A, RS and SR are glide reflections, if A is not on m, and a line reflection otherwise.

Again define p as the line through A perpendicular to m. But this time let n be the line through A so that S = R_pR_n. Let P and be the intersections of p and n, respectively, with m. Then by construction angle NAP = (1/2) rotation angle of S.

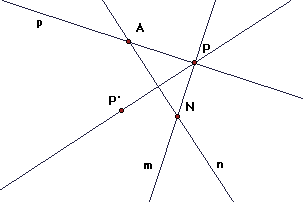
So the composition SR = R (R_pR_n) = (RR_p)R_n = H_PR_n, for the lines p and m are perpendicular at P, so the double line reflection is the half turn with center P.

But this shows that SR is the composition of a line reflection and a halfturn, so by the previous step this is the glide reflection G_P'P for P' = R_n(P). (This is a line reflection if A is on m, so that A = P.) So the invariant line is the perpendicular to n through P and the glide vector if P'P.

In the same way, one can show that RS is the glide reflection G_pp*, where P* is the reflection of P in line AQ = q, where Q is the reflection of n and q is the reflection of n, both in line p. For this line q, S = R_qR_p since the angle PAQ = angle NAP.

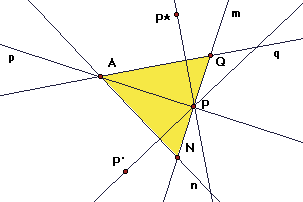
Also notice that S(N) = Q, since angle NAQ = angle of rotation of S. The triangle NAQ is isosceles with altitude AP.

Step 3. Suppose u, v, w are three lines that are neither concurrent nor parallel. Then the composition of the 3 line reflections R_wR_vR_u is a glide reflection.

The lines form a triangle or else two are parallel and the other line is a transversal. If u and v intersect, call the intersection point A. By hypothesis A is not on w. In the case that u and v are parallel, then v and w intersect at a point B not on u.

Assume the first case that A exists. Then R_vR_u is a rotation S with center A, and R_wR_vR_u = R_wS is the glide reflection from Step 2.

If B exists, then R_wR_vR_u = UR_u, where U = R_wR_v is a rotation centered at B. Again by step 2 this is a glide reflection.

QED

Notice that the construction is quite explicit. For example, given a triangle ABC, let R₁, R₂, R₃ be reflection in the lines BC, CA, AB. Then by the theorem, R₁R₂R₃ is a glide reflection.

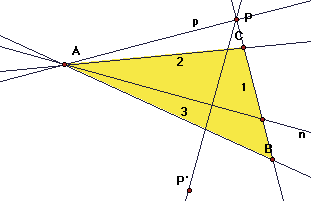
To find the invariant line and glide vector, observe that R₂R₃ is a rotation S centered at A. We "mirror move" these two lines to write the rotation as the product of two different lines. Let p be the altitude of ABC through A. Then p is perpendicular to BC. Construct line n so that R_pR_n = S. If n intersects line BC at N, then oriented angle NAP = angle BAC.

Now as in the proof, R₁R₂R₃ = R₁S = R₁R_pR_n = H_PR_n = G_P'P = G, a glide reflection, where P' is the reflection of P in n. In the figure, P is the foot of the altitude and the invariant line of G is the perpendicular to BA through P. The glide vector is P'P.

Note: This proof is also given as an exercise in Brown.