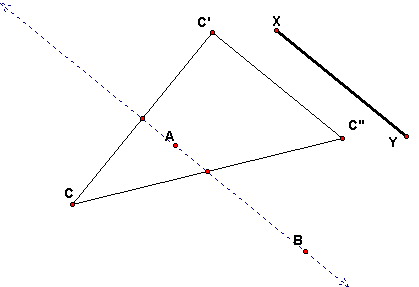
Definition. Suppose m is a line and AB is an oriented segment parallel to m.
Let the glide transformation with invariant line m and glide vector AB be the transformation G that takes any point C to a point C'' defined as follows: let C' be the reflection of C across m and C'' be the translation of C' by vector AB.
In this figure the translation is given by a vector AB where A and B are both on m. The same C' and C'' are give if we translate by a vector such as XY in the figure, which is parallel to m and determines the same translation as AB.

The important geometry here is this:
a) Triangle CC'C'' is a right triangle with hypotenuse CC''.
b) Line m is the perpendicular bisector of one of the legs.
c) Therefore, m intersects CC'' in M, the midpoint of CC'' by Thales theorem.
d) If we reverse the order of translation and reflection we get the same C'', i.e., if C''' is the translation of C by AB the reflection of C''' in m is C''. This only is true because the vector is parallel to m, so the quadrilateral CC'C''C''' is a rectangle.
From the definition it is clear that the only line n for which G(n) = n is the line n = m. That is why m is called the invariant line. It is invariant under G, this means that G is a symmetry of the line. G is not a symmetry of any other line.
It is clear from the definition that the composition GG is the translation by 2AB. It is also clear that GGG is the glide reflection with invariant line m and glide vector 3AB, etc.
An important consequence of (c) is this
Proposition: If G is a glide reflection, for any point C, the midpoint of the segment from C to G(C) is on the invariant line m.
The importance of this fact is that when we are given G in some indirect way, it is possible to construct G from midpoints of points and their images. For example, these two congruent "flags" are related by a glide reflection. The invariant line can be constructed from two midpoints of segments connecting a point and an image.

To construct the glide vector once the invariant line is known is straightforward. In this figure, if one knows C and C'' and the dashed line m, one constructs C' as the intersection of the line through C perpendicular to m and the line through C'' parallel to m. Then the vector C'C'' is the glide vector.

Given any two congruent figures such as the two flags above, one can find either one, two, or three line reflections so that the composition of the reflections takes one flag to the other. (See Brown Theorem 11 for how to transform one triangle to a second congruent triangle. Once a triangle is transformed, the rest of the figure follows by Theorem 10.) It is also proved that if 3 lines are not concurrent or parallel, that the composition of these 3 line reflections is a glide reflection. (Brown, Theorem 12, plus problems 17, 18, 19 on pp. 53.)
However, knowing the 3 line reflections still leaves quite a bit of work to find the invariant line and the glide vector (Brown, problem 19, page 54 and class discussion). If a transformation G is known to be a glide reflection, then the midpoint method above is one way to find this defining data directly.