Thales Theorem and Figure

A key and frequently-occurring figure in the theory of similar triangles is a figure with two parallel lines adn two intersecting transversals. In this course we will refer to this figure as a Thales Figure, in honor of the early Greek geometry who allegedly measure the height of the Great Pyramid using shadows.

Thales Theorem

Given two lines AB and CD. When AC and BD intersect at a point E, and when E is either (1) a point interior to both segment AC and segment BD or else (2) exterior to both segments, then the triangles AEB and CED (1) share the angle AEB = angle CED or else (2) these two angles are vertical angles. Then for such a figure,

• Line AB is parallel to line CD if and only if
• Triangle AEB is similar to triangle CED if and only if
• EC/EA = ED/EB

Proof: This is BG problem 4.3 (in Assignment 4), except that this problem is not quite correct as stated, since it is false if E is interior to segment AC and exterior to segment BD.

Comment: The theorem is true as stated in BG if we allow NEGATIVE RATIOS of segments when the oriented segments point in opposite directions. Then the two ratios are positive in case (1) and negative in case (2) and the theorem is true as stated in BG without assuming (1) and (2) above.

Thales Figure

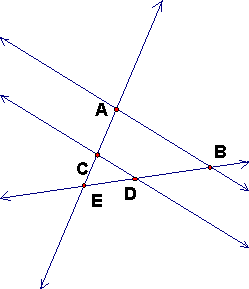
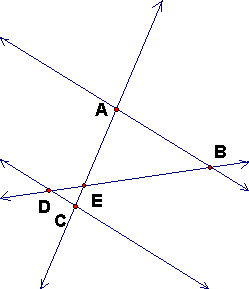
If any of these conditions (and hence all of these conditions) is true, then we call the figure a Thales figure. These figures show cases (1) and (2). Interactive Java Sketchpad figures that show the signed ratio are at this link.

A and C are on the same side of E.(and thus B and D are on the same side of E). Another way of saying this is that C is on ray EA or that ray EA = ray EC. In this case EC/EA > 0 and ED/EB > 0.	The interesection E is between A and C (and thus between B and D). Another way of saying this is that the rays EA and EC are opposite rays. In this case EC/EA < 0 and ED/EB < 0.