Various Proofs of The Pythagorean Theorem
by Area and/or Algebra
In all that follows, we will work with a right triangle and label the leg lengths
as a and b and the hypotenuse as c.
- Compute the area of the big square, the triangle and the smaller square.
Then use algebra to relate a, b, and c.

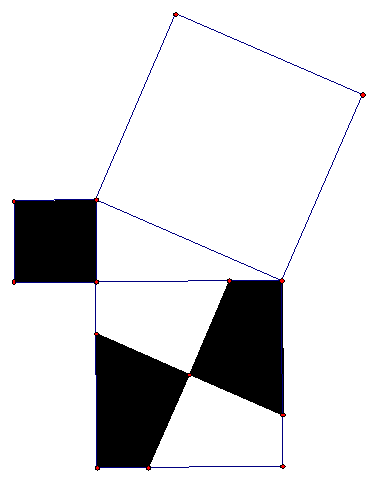
- Take the same figure as above, and think of the corner triangles as moveable.
Rearrange the "furniture" to get this figure. Without algebra,
explain why the sum of the areas of the interior squares in this figure equals
the area of the interior square above. Conclude the Pythagorean Theorem.

- Relate the area of the outside square to the inside pieces and use algebra
to deduce the Pythagorean Theorem.
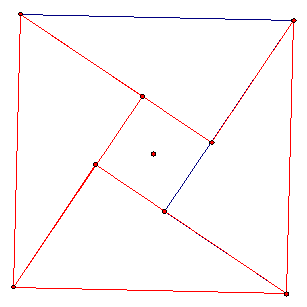
- This Chinese Figure Relates the areas of rectangles to squares. It also
can be used to find the Pythagorean Theorem again, using algebra.

- This is the figure for President Garfield's proof. Deduce the theorem by
computing the area of the trapezoid and then the area of the 3 triangles inside.

- In this dissection proof the trick is to cut apart the triangle on the larger
leg into 4 pieces. Then assemble these 4 quadrilaterals and the square on
the other leg to make the square on the hypotenuse. This is nice to do as
a puzzle, but there is some work to do to prove that the puzzle really fits
exactly.
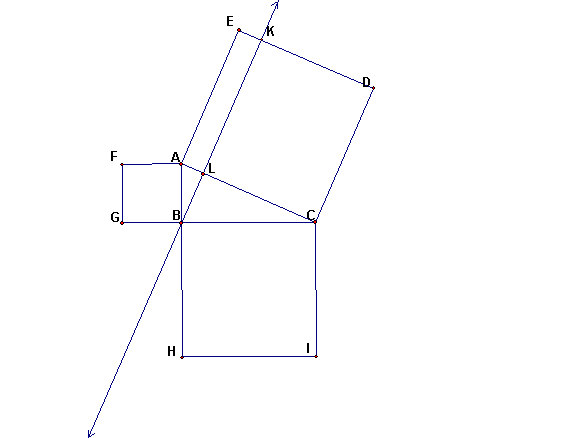
- The next figure does not use area dissection directly, nor algebra. It
is the figure for the proof in Euclid's Elements. Part of the proof is to
show triangle AFC is congruent to triangle ABE by SAS. Then we observe that
2 * area AFC = area square ABGF. (Tell why!) Also 2 * area ABE = area rectangle
ALKE. So area rectangle ALKE = area of one the square with side a. Likewise
the rectangle CDKL = area of the square with side b. But the two rectangles
together make up the square with side c.