Trapezoids
Definition of Trapezoid


Believe it or not, there is no general agreement on the definition of a trapezoid. In B&B and the handout from Jacobs you got the Exclusive Definition.
Exclusive Definition of Trapezoid
A quadrilateral having two and only two sides parallel is called a trapezoid.
However, most mathematicians would probably define the concept with the Inclusive Definition.
Inclusive Definition of Trapezoid
A quadrilateral having at least two sides parallel is called a trapezoid.
The difference is that under the second definition parallelograms are trapezoids and under the first, they are not.
The advantage of the first definition is that it allows a verbal distinction between parallelograms and other quadrilaterals with some parallel sides. This seems to have been most important in earlier times. The advantage of the inclusive definition is that any theorem proved for trapezoids is automatically a theorem about parallelograms. This fits best with the nature of twentieth-century mathematics.
It is possible to function perfectly well with either definition. However, it is important to have agreement in a math class on the definition used in the class.
In Math 444 the official definition of a trapezoid is the Inclusive Definition. In the event we wish to distinguish trapezoids with exactly two parallel sides, we will call such trapezoids strict trapezoids.
Diagonals of Trapezoids
Let ABCD be a trapezoid. Construct point E as the intersection of the diagonals AC and BD. By the diagonals are transversals, so the marked angles are equal: angle BAE = angle DCE and angle ABD = angle CDE. Thus by AA, the triangles ABE and CDE are similar.
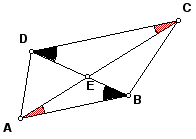
Theorem
Given a trapezoid ABCD with parallel sides AB and CD, let E be the intersection of the diagonals AC and BD. If we label as r the ratio r = AB/CD, then the diagonals are divided by this ratio; AE/CE = BE/DE = r.
Proof. Since the triangles ABE and CDE are similar, then these are ratios of corresponding sides.
Application to a Construction Problem
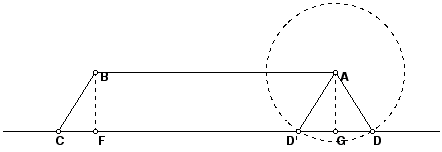
If a and b are positive numbers and MN is a segment, to construct a point P so that MP/NP = a/b, construct two lines m and n perpendicular to MN, one through M and one through N. Construct a point M' on m and a point N' on n, with M' and N' on opposite sides of line MN, so that MM'/NN/ = a/b. For example, if a and b are lengths that have been constructed, then construct M' and N' with MM' = a and NN' = b. Or if a and b are integers, mark of a equal distances to make MM' and b of the same unit of distance to make NN'. Here is an example constructing a point P that divides MN into segments of length 2/9 and 7/9, thus in the ratio 2/7.
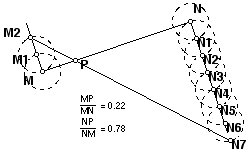
Here are some other theorems about ratios and trapezoids that will be discussed in class.
Theorem
Given a trapezoid ABCD with parallel sides AB and CD, with E the point of intersection of the diagonals AC and BD. If k is any line through E intersecting AB in P and CD in Q, then AP/BP = CQ/DQ.
Corollary
Given a trapezoid ABCD with parallel sides AB and CD. The midpoints of AB and CD are collinear with the point of intersection of the diagonals.
Theorem
Given a trapezoid ABCD with parallel sides AB and CD, with E the point of intersection of the diagonals AC and BD. If e is the line through E parallel to AB, then if e intersects BC in F and DA in G, the ratios BF/CF = AG/DG = AB/CD.
Theorem
Given a trapezoid ABCD with parallel sides AB and CD. If M is the midpoint of BC and N is the midpoint of CD, then the line MN is parallel to AB and CD.
Isosceles Trapezoids
A trapezoid ABCD with parallel sides AB and CD is called an isosceles trapezoid if it is a strict trapezoid with BC = DA. Notice that if ABCD is a parallelogram, it is a (non-strict) trapezoid with BC = DA.
Theorem
Given a trapezoid ABCD with parallel sides AB and CD. ABCD is an isosceles trapezoid if and only if the base angles DAB and CBA are equal.
Proof: Start by constructing perpendiculars BF and AG as in this figure. Show that given ABC, at most two points D and D' are possible as the fourth vertex.