m308 a97 major quiz 1

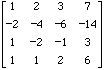
Instructions: Do all problems. Show your work. Answer on the test pages.

Conditions: Closed book, no notes, no calculator.

Time: 50 minutes.

A Helpful Fact that is true.

Use it in Part I, problems 1A-1E.

The matrix

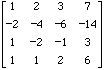
can be transformed by elementary row operations to the row-equivalent matrix

N =

Part I.

1A. Compute the reduced row echelon form of the matrix M.

Let , , , .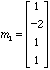

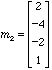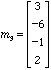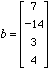1B. Solve the matrix equation Mx =b. Write the solution x, if there is one, as a vector in parametric form.

1C. Solve the matrix equation Mx = 0. Write the solution x, if there is one, as a vector in parametric form.

1D. Are the vectors m1, m2, m3 linearly independent? Show this concretely, by a numerical relation based on the definition..

Part II. True or False. Give a brief reason or convincing example or counter-example for each answer.

2A. A homogeneous equation is always consistent.

2B. The equation x = p + tv describes a line through v parallel to p.

2C. The solution set of Ax = b is the set of all vectors of the form w = p + vh, where vh is any solution of the equation Ax = 0 and Ap = b.

2D. Any set of 4 vectors in R3 must be linearly dependent.

2E. Any set of 3 vectors in R4 must be linearly independent.

Part III.

A is a matrix and b is a vector. Suppose that the set of all solutions x of the equation Ax = b is the set 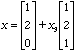, for all x3.

3A. What is the set of solutions of Ax = 0?

3B. Is it true that the set of solutions of Ax = b is 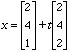, for all t? Explain.