Homework 7 (due Friday, 12/4 at the start of class)

For these problems, follow these instructions, which include a little more than the instructions in the book.

Steps 1 and 2 are essentially what the book calls for in most cases. Steps 3 and 4, especially 4, will be spelled out in a handout that you will get Wednesday (and that will appear on the website by then). You won’t lose any time by going ahead and solving for (1) and (2) now, since after that (3) and (4) are just a matter of observing and writing down information from your solutions – no more real work.

(1) Find all the eigenvalues of matrix A. (Either one or two for these problems.)

(2) Solve for all the eigenvectors for each eigenvalue.

(3) For the nxn matrix A in the problem, write down a basis {S₁, S₂, ... , S_n} of Rⁿ consisting of eigenvectors of A – if such a basis exists.

(4) Write an equation of matrices, AS = SD, where A is the matrix in the problem, S is the matrix with columns S₁, S₂ and D is a diagonal matrix. Check that your equation is correct by multiplying both sides and comparing.

Hint: When computing the roots of the characteristic polynomial of a 3x3 matrix, if the determinant comes out in partially factored form (e.g., (x-5)(x² + 3x + 2)), use this factorization! DO NOT multiply it all out and then start factoring. One of your factors in this example is (x-5) already!

7.1: Section 4.1, #2

7.2: Section 4.1, #4

7.3: Section 4.1, #6

7.4: Section 4.1, #8

7.5: Section 4.4 #8

7.6: As in Section 4.4 Matrix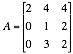

7.7: Section 4.5 #14

7.8: Section 4.5 #10, 11 (both the same matrix, do steps 1- 4 above)