Equations of a Curve Space: A Spiral

These are pictures/animations to visualize the vector and parametric equations of a curve. The curve is a spiral. The first two animations may take a while to load.

The first picture represents the vector equation r(t)=<cos(t),sin(t), t>.The animation is from t=-20 to t=20.

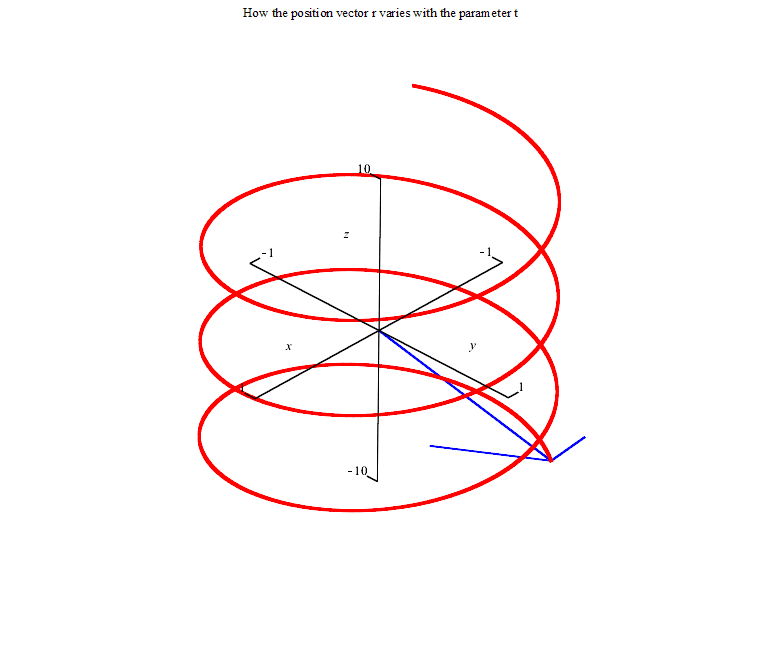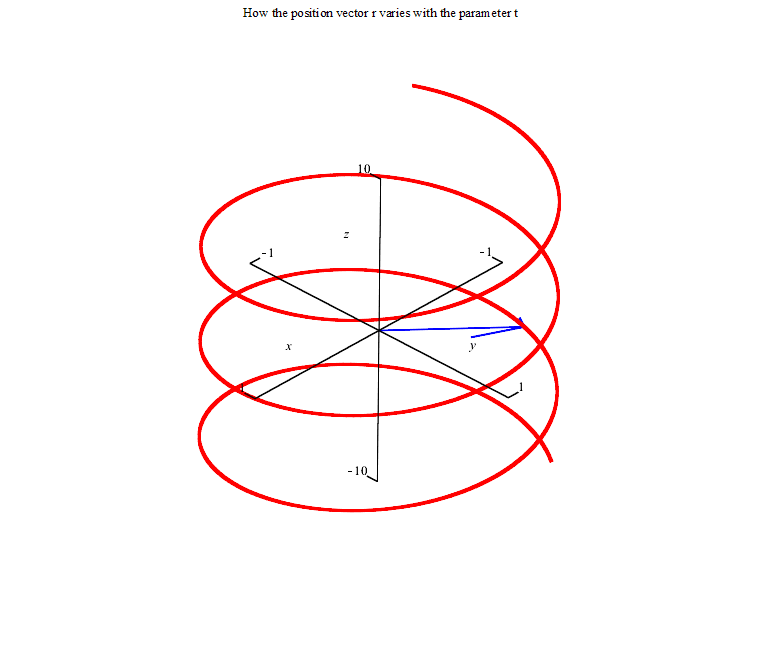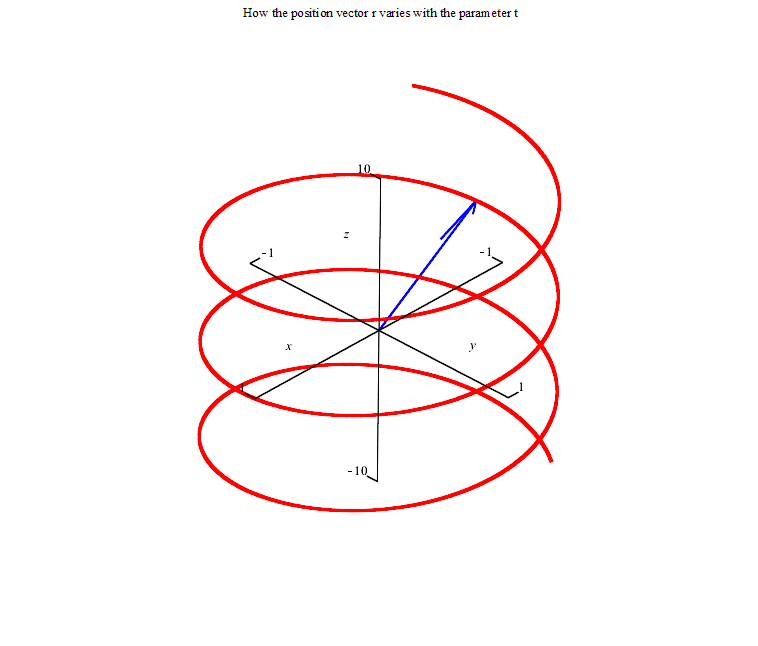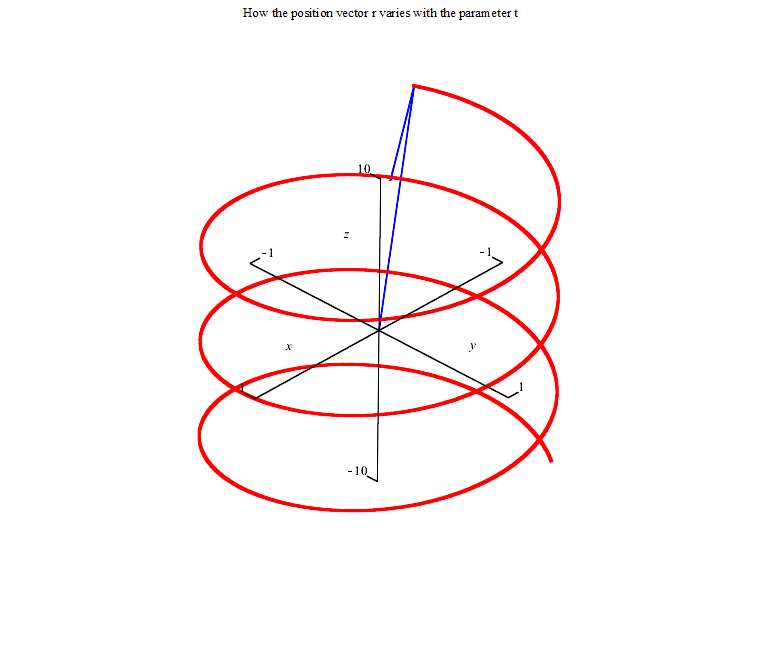
The second picture represents the parametric equations. The point (cos(t),sin(t),t) varies with t. The animation is again from t=-20 to t=20.

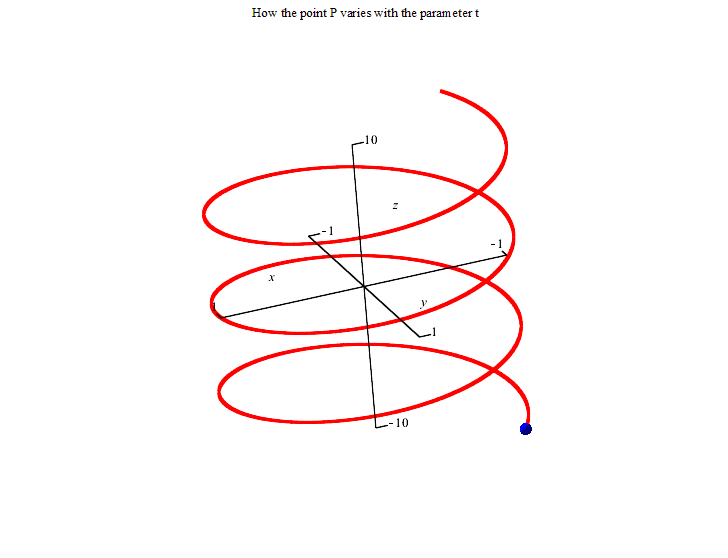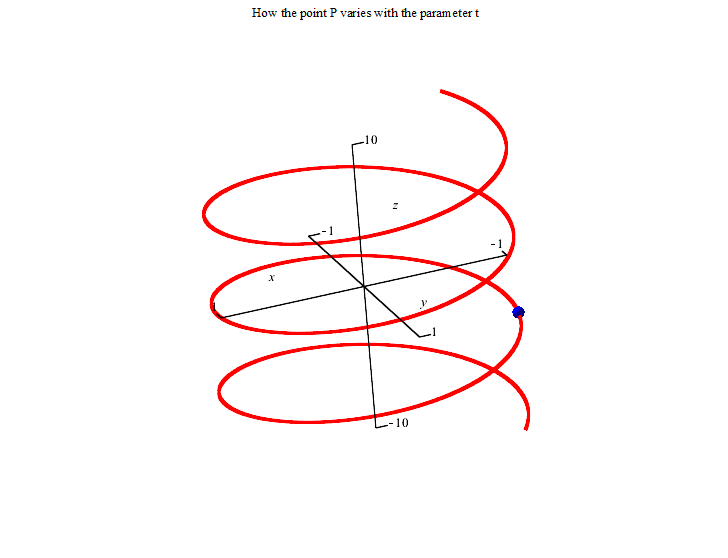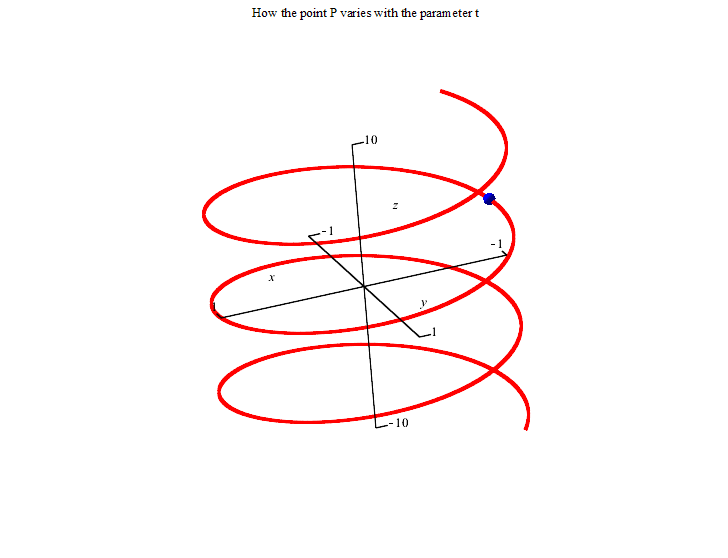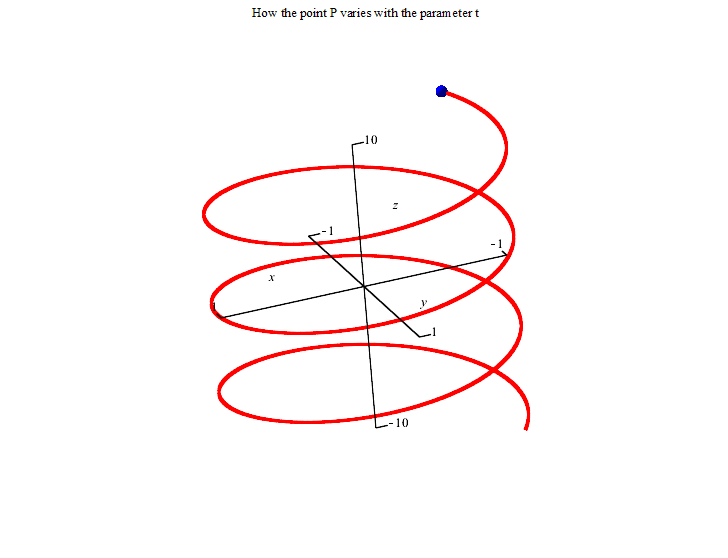
The spiral sits on three surfaces as shown below. The arbitrary point (cos(t),sin(t),t) on the spiral satisfies all three surface equations regardless of the value of t. So all points of the spiral are on each of those surfaces. You can get the equations of the surfaces by trying to eliminate the t in the equations.

A curve in space can also be described as the intersection of two surfaces. Below is the spiral as the intersection of two of the surfaces above.