Pathological Taylor Series Examples

The function

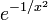
serves as an important example of the fact that Taylor series representations of functions based at certain points are not always possible.

If we let f(x) equal this function for x not equal to 0, and set f(0)=0, then f is continuous for all x and has derivatives of all orders that are continuous everywhere (this is left as an exercise).

Here is a graph of the function near x=0:

If we try to create the Taylor series for this function based at b=0, one can show that f^(k)(0)=0 for all k. That is, every derivative of f(x) is equal to 0 at 0.

We might say, rather casually, that y=f(x) is very, very flat at x=0.

The result of this is that the Taylor series for f based at b=0 is identically zero. Clearly, this is not a very useful series representation: it only converges (i.e. is equal to f(x)) at the single point x=0.

A little investigation of the derivatives of f will show that there is more going on than just the fact that the derivatives are all zero at x=0.

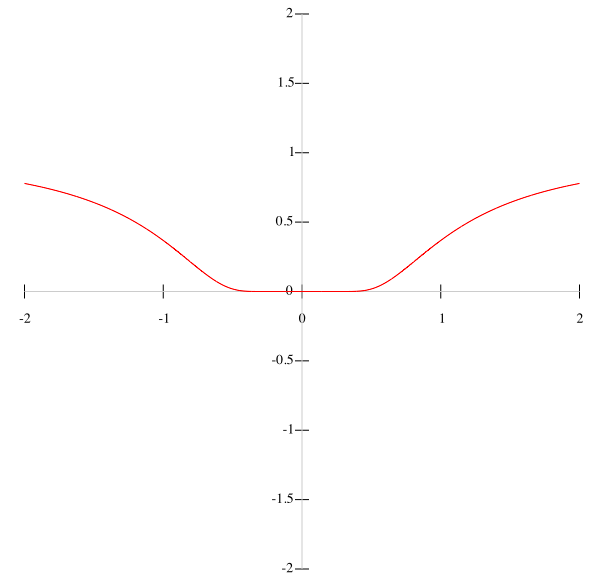
Here is the first derivative:

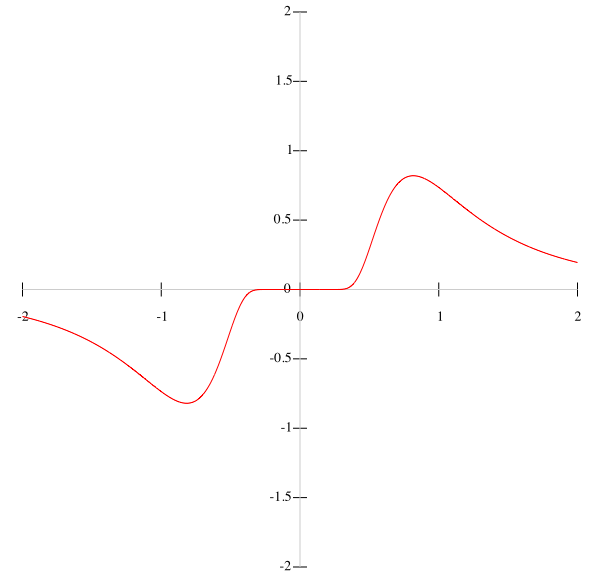
Here is the second derivative (note the change of the vertical scale):

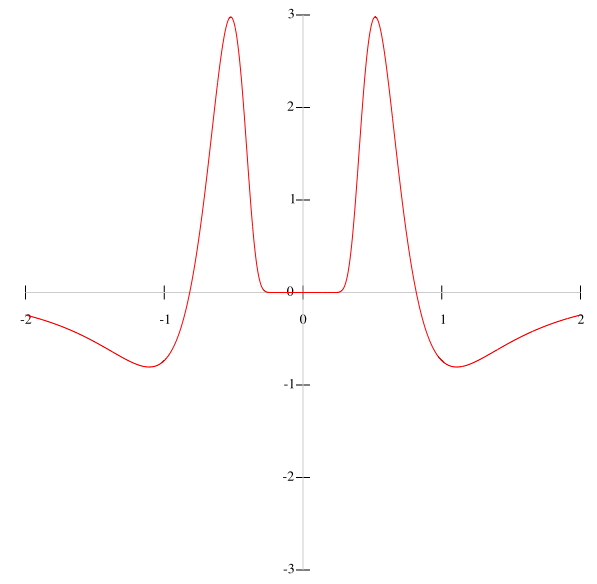
Here is the third derivative (note the change of the vertical scale):

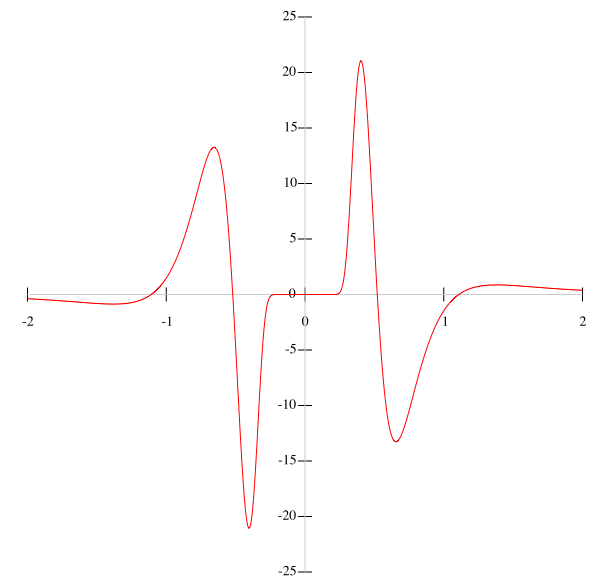
Here is the fourth derivative (note the change of the vertical scale):

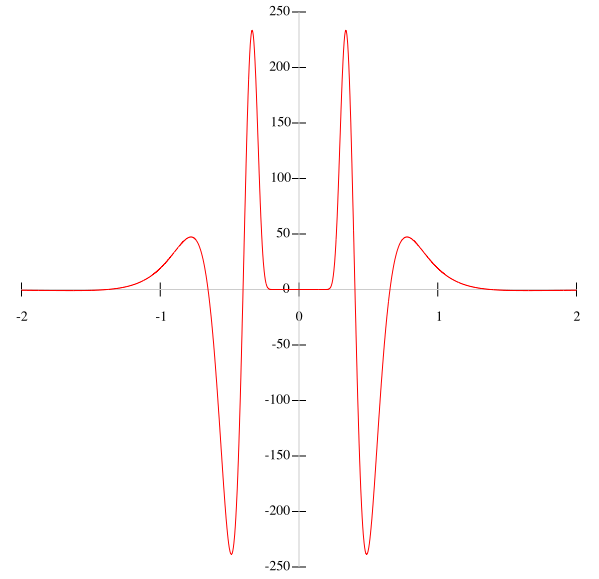
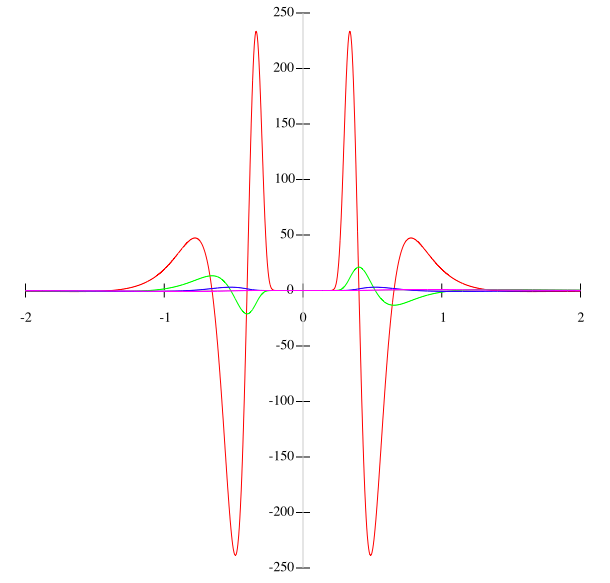
As you can see, the peaks get drastically larger and they occur closer and closer to x=0. This is part of the reason for the poor convergence of the Taylor series: in any interval around zero, you will find extreme growth in the maximal values of the n-th derivative as n goes to infinity. The upshot of this behavior for this function is that the series cannot converge in any interval around zero (except the trivial interval of x=0 itself).

Here are those derivative graphs all on the same axes for comparison: