Center of Mass with Polar Integration Example

Consider the polar region R bounded by m ≤ r ≤ 1, 0 ≤ θ ≤ π/2. (We might call this a polar rectangle, since the bounds are constants, as they would be on x and y for a cartesian rectangle with sides parallel to the axes.)

If we assume constant density, what is the center of mass of such a region?

We have to calculate three quantities: the mass, and the moments with respect to the x and y axes.

If we assume a constant density ρ, then the mass is just ρ times the area:

The moments are calculated like this:

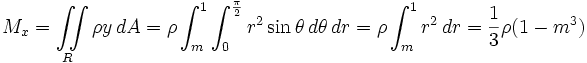
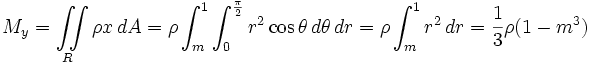
The center of mass is thus

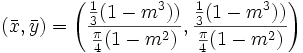
The animation below shows the situation for various values of m. The crossing black lines intersect at the center of mass. You can see that initially the center of mass is inside the region, but as m increases, the center of mass moves more slowly than the boundary at r=m, so eventually the center of mass is outside the region.

In the animation, you can see the transition happen somewhere between m=0.8 and m=0.85.

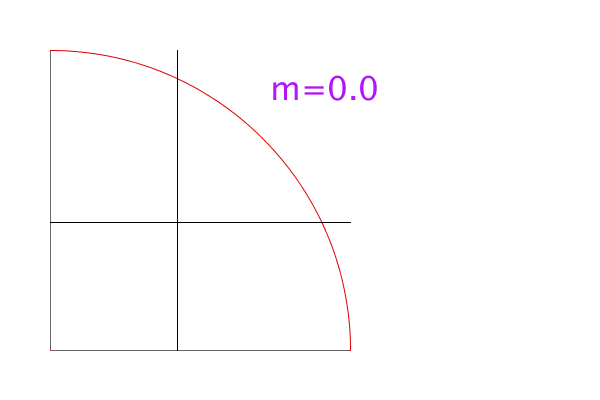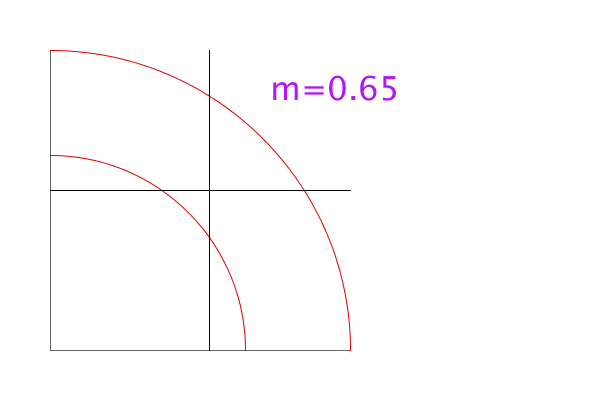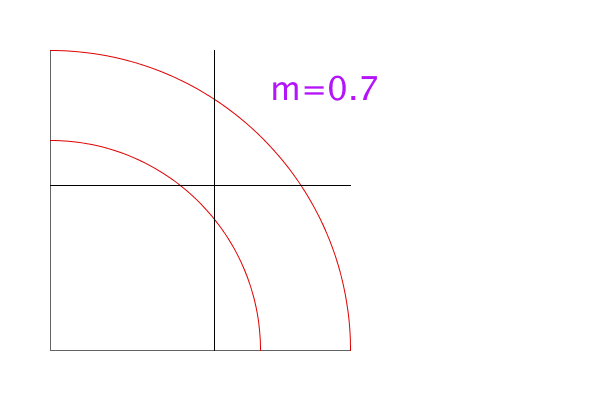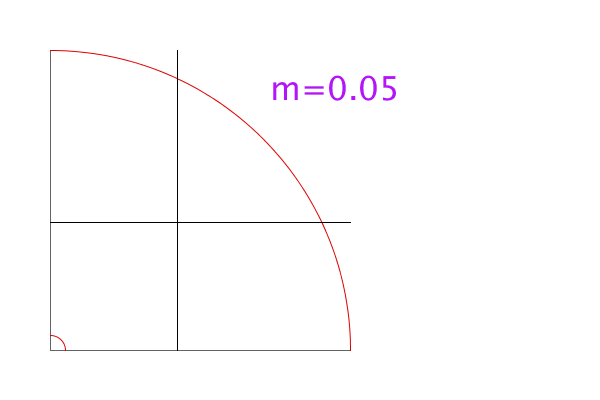
When exactly does the center of mass leave the region? The center of mass will be outside the region if the distance from the center of mass to the origin is less than m. That is, if

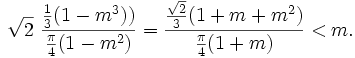
This is equivalent to

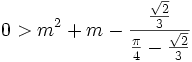
Solving this, you can find that the center of mass is outside the region if m > 0.82337397...