Weierstrass functions are famous for being continuous everywhere, but differentiable "nowhere". Here is an example of one:
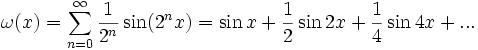
It is not hard to show that this series converges for all x. In fact, it is absolutely convergent. It is also an example of a fourier series, a very important and fun type of series. It can be shown that the function is continuous everywhere, yet is differentiable at no values of x.
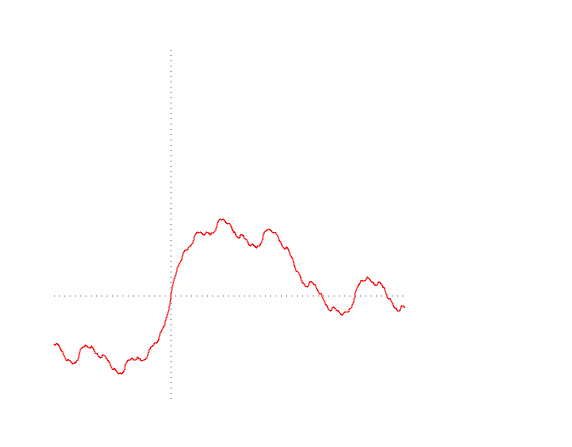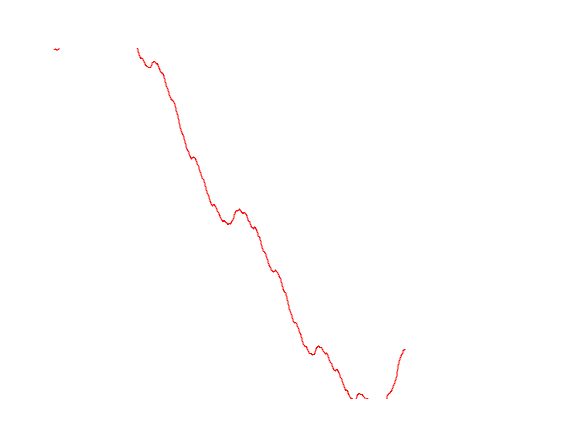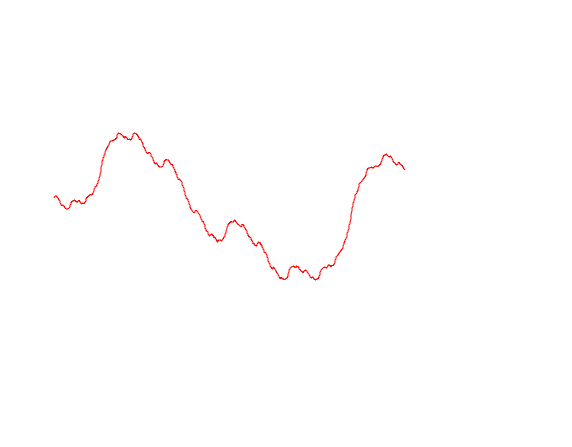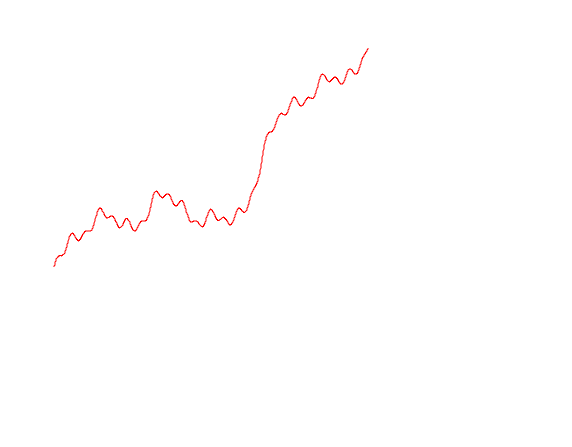
Here's a graph of the function. It is periodic with period 2π.
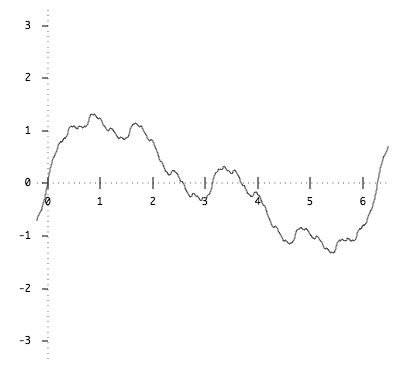
You can see it's pretty bumpy. So bumpy, in fact, that it's not differentiable anywhere.
Below is an animation, zooming into the graph at x=1. The graph zooms in quite a ways, and you can see that the graph does not become smooth, or linear, as a differentiable function does. However, at the last frame, the graph looks rather smooth due to computational limits of the software used, but theoretically one could zoom in forever and it would never become smooth or linear.
Wikipedia and MathWorld both have informative entries on Weierstrass functions.
back to Dr. Conroy's Math Department Page