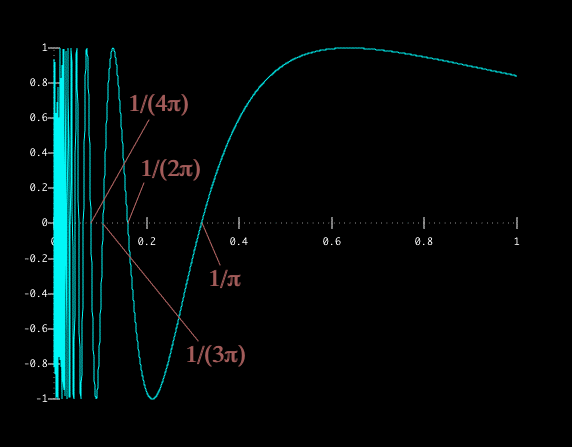
There are an infinite number of these pairs, and they are all between 0 and 1/pi. What's more, there are only finitely many between any positive x value and 1/pi, so there must be infinitely many between that x and 0.
The behavior of the functions sin(1/x) and x sin(1/x) when x is near zero are worth noting.
Below are plots of sin(1/x) for small positive x.
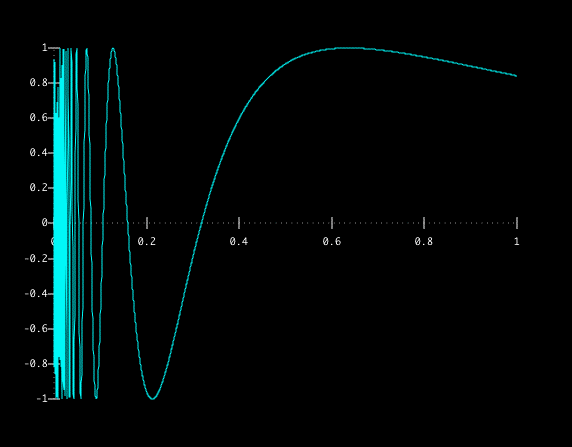
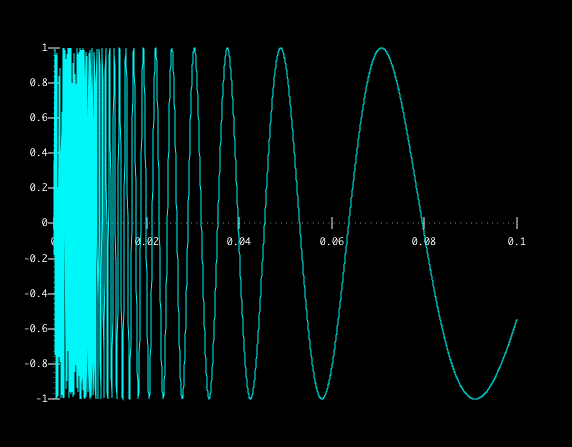
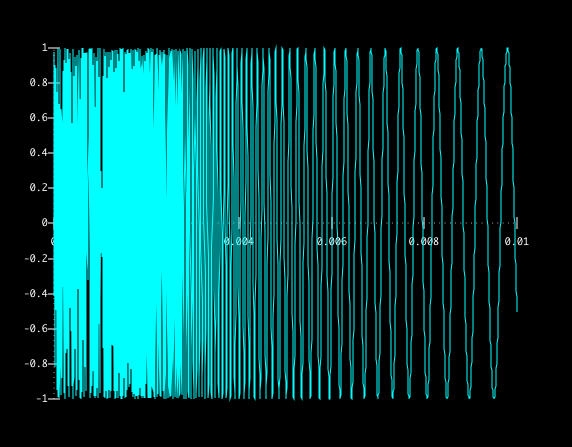
We can see that as x gets closer to zero, the function keeps wobbling (or oscillating) back and forth between -1 and 1.
In fact, sin(1/x) wobbles between -1 and 1 an infinite number of times between 0 and any positive x value, no matter how small.
To see this, consider that sin(x) is equal to zero at every multiple of pi,
and it wobbles between 0 and 1 or -1 between each multiple.
Hence, sin(1/x) will be zero at every x = 1/(pi k), where k is a
positive integer. In between each consecutive pair of these values, sin(1/x)
wobbles from 0, to -1, to 1 and back to 0.

There are an infinite number of these pairs, and they are all between 0 and 1/pi.
What's more, there are only finitely many between any positive x value and
1/pi, so there must be infinitely many between that x and 0.
We can conclude that as x approaches 0 from the right, the function sin(1/x) does not settle down on any value L, and so the limit as x approaches 0 from the right does not exist.
Now, the function x sin(1/x) is a somewhat different story.
Since x approaches zero as x approaches zero,
multiplying sin(1/x) by it will result in another quantity that approaches zero.
Below is some visual evidence. The yellow lines are y=x and y=-x, while the
blue curve is x sin(1/x):
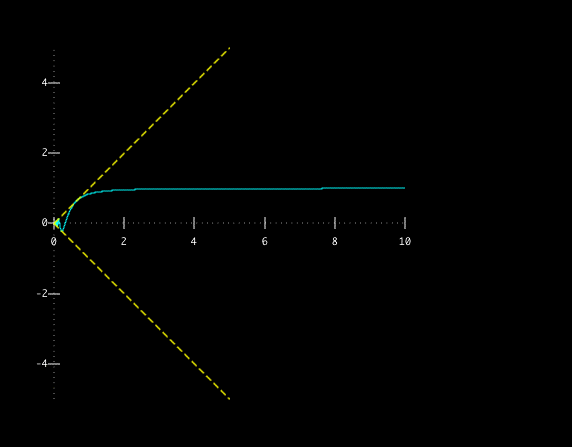
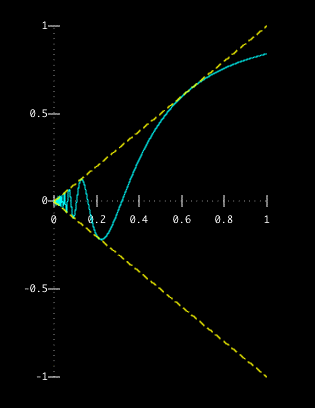
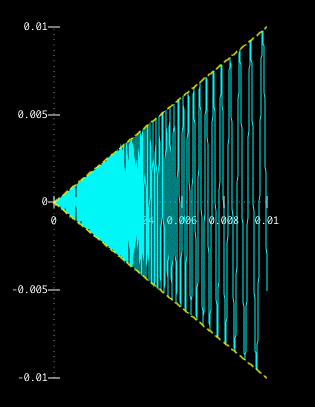
This is an example of what's known as the Sandwich Theorem.
The Sandwich Theorem says that
if g(x) ≤ f(x) ≤ h(x), and
g(x) and h(x) both approach L as x approaches a,
then f(x) must also approach L as x approaches a.
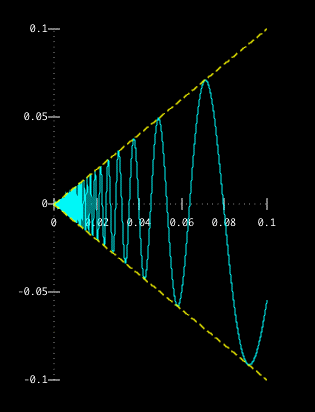
In this case, we know that, since -1 ≤ sin(1/x) ≤ 1, we can conclude that -x ≤ x sin(1/x) ≤ x for positive values of x. Then, since x and -x both approach 0 as x approaches 0 from the right, so must x sin(1/x).
You can make a similar argument from the left, and conclude that
the limit as x approaches 0 of x sin(1/x) is 0.
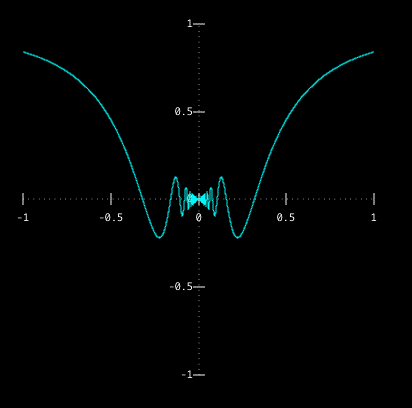
Here's a picture that shows the goings on to the left of zero.
back to Dr. Conroy's UW page