A Box Folding Problem
(Though this is a classic calculus problem, it illustrates some ideas useful at the precalculus level.)
Suppose you have a 1 meter by 1 meter sheets of flat metal. You want to make an open-top box from it by cutting identical squares from each corner and folding the result.
The animation below shows the result of cutting squares (blue) from the corners of the metal sheet (the yellow square) and then folding the resulting yellow bits up into a box (colored pink). The grey cube on the right has the same volume as the pink box.

We can see that the volume of the resulting box is not constant: it depends on the size of the square that is cut from the corners.
Let x be the length of a side of the square cut from each
corner (i.e., the blue squareis).
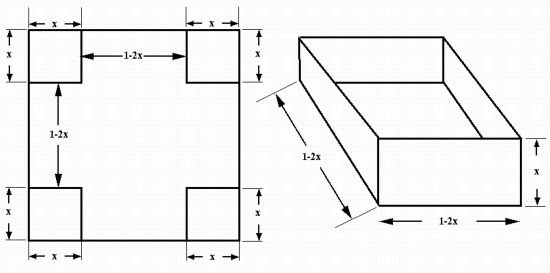
Then the volume of the box is
V(x) = x(1-2x)(1-2x) = 4x3-4x2+x.
Below is a graph of V(x).
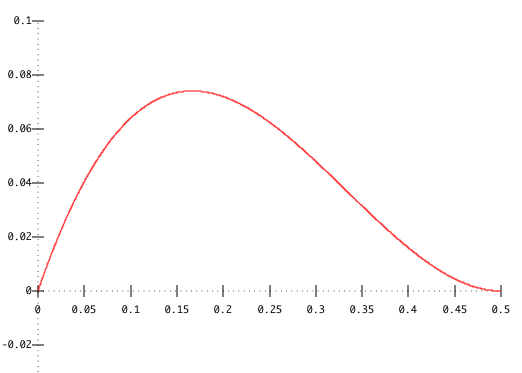
We can see that the maximum volume happens
when x is about 0.15. With calculus you can prove that
the maximum occurs exactly at x=1/6.