WXML Winter 2020
Number Theory and Noise
Thien Do, Pubo Huang, Ally Krinsky,
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
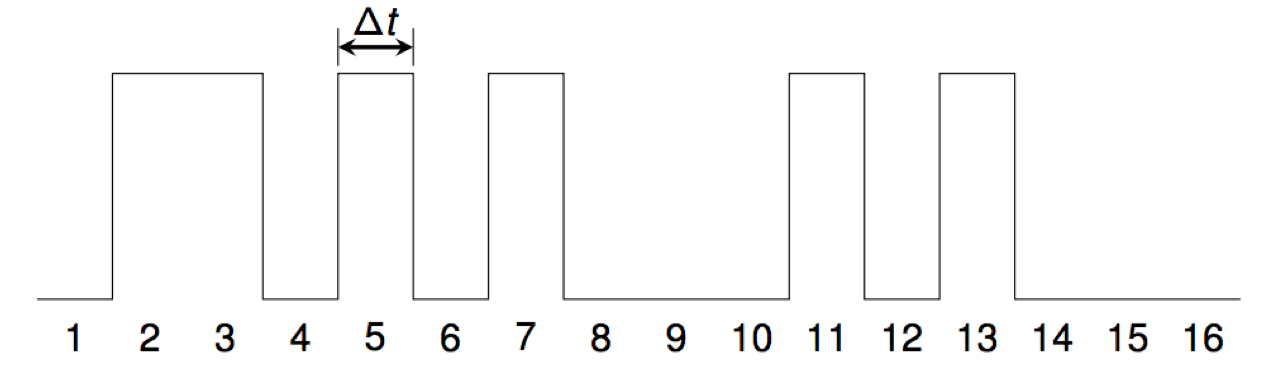
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | download | creator | quarter | tags | comments |
|---|---|---|---|---|---|---|---|
| A000037 | Numbers that are not squares (or, the nonsquares). | download | Ally Krinsky | Win2020 | |||
| A002328 | Numbers n such that n^2-n-1 is prime. | download | Ally Krinsky | Win2020 | |||
| A002642 | Numbers n such that (n^2+n+1)/3 is prime. | download | Ally Krinsky | Win2020 | |||
| A002643 | Numbers n such that (n^2+n+1)/19 is prime. | download | Ally Krinsky | Win2020 | |||
| A002644 | Numbers n such that (n^2+n+1)/21 is prime. | download | Ally Krinsky | Win2020 | |||
| A002731 | Numbers n such that (n^2+1)/2 is prime. | download | Ally Krinsky | Win2020 | |||
| A002733 | Numbers n such that (n^2 + 1)/10 is prime. | download | Ally Krinsky | Win2020 | |||
| A002970 | Numbers n such that 4*n^2 + 9 is prime. | download | Ally Krinsky | Win2020 | |||
| A004083 | Numbers n such that cos(n-1) <= 0 and cos(n) > 0. | download | Ally Krinsky | Win2020 | |||
| A002640 | Numbers n such that (n^2 + n + 1)/3 is prime. | download | Ally Krinsky | Win2020 | |||
| A002641 | Numbers n such that (n^2 + n + 1)/7 is prime. | download | Ally Krinsky | Win2020 | |||
| A002642 | Numbers n such that (n^2 + n + 1)/7 is prime. | download | Ally Krinsky | Win2020 | |||
| A002643 | Numbers n such that (n^2 + n + 1)/7 is prime. | download | Ally Krinsky | Win2020 | |||
| A004614 | Numbers that are divisible only by primes congruent to 3 mod 4. | download | Ally Krinsky | Win2020 | |||
| A007519 | Primes congruent to 1 mod 8. | download | Ally Krinsky | Win2020 | primes | ||
| A007520 | Primes congruent to 3 mod 8. | download | Ally Krinsky | Win2020 | primes | ||
| A007521 | Primes congruent to 5 mod 8. | download | Ally Krinsky | Win2020 | primes | ||
| A001000 | a(n) = least m such that if a/b < c/d where a,b,c,d are integers in [0,n], then a/b < k/m < c/d for some integer k. | download | Thien Do | Win2020 | |||
| A001748 | 3*primes. | download | Thien Do | Win2020 | |||
| A001750 | 5*primes. | download | Thien Do | Win2020 | |||
| A001915 | Primes p such that the congruence 2^x = 3 (mod p) is solvable. | download | Thien Do | Win2020 | primes | ||
| A002970 | Numbers n such that 4*n^2 + 9 is prime. | download | Thien Do | Win2020 | |||
| A100317 | Numbers k such that exactly one of k - 1 and k + 1 is prime. | download | Thien Do | Win2020 | |||
| A004759 | Binary expansion starts 111. | download | Thien Do | Win2020 | |||
| A006532 | Numbers n such that sum of divisors of n is a square. | download | Thien Do | Win2020 | |||
| A014580 | Binary irreducible polynomials (primes in the ring GF(2)[X]), evaluated at X=2. | download | Thien Do | Win2020 | |||
| A015782 | Phi(n) + 3 divides sigma(n + 3). | download | Thien Do | Win2020 | |||
| A024917 | a(n) = Sum_{k=2..n} k*floor(n/k). | download | Thien Do | Win2020 |