WXML Winter 2018
Number Theory and Noise
Nile Wymar, Sherry Chen, Robert Pedersen, Hongyu Cao
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
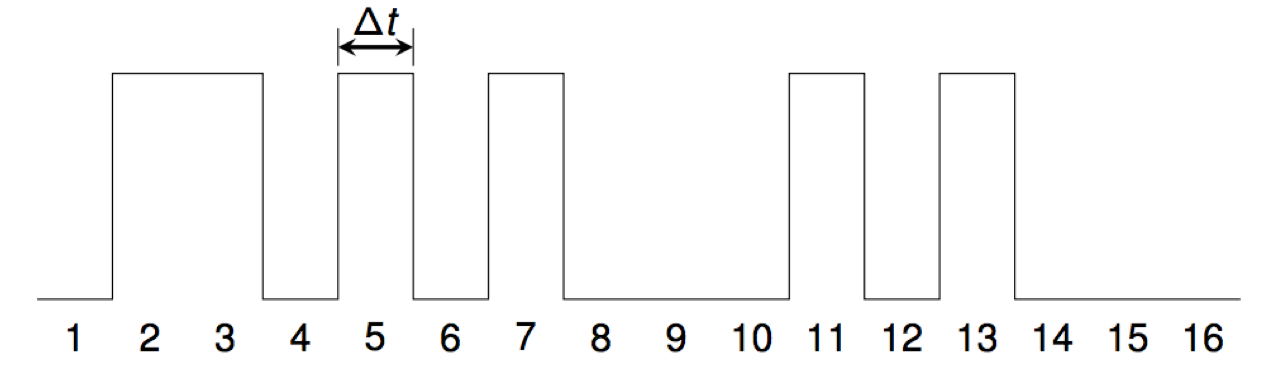
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | creator | |
| n such that the sum of digits of n^3 is one more than a cube | download | Nile Wymar | ||
| n such that sum of digits of n^4 is a fourth power | download | Nile Wymar | ||
| n such that sum of digits of n^2 equals 54 | download | Nile Wymar | ||
| n such that sum of digits of n^3 equals 80 | download | Nile Wymar | ||
| n such that sum of digits of n^4 equals 99 | download | Nile Wymar | ||
| A004207 | a(0) = 1, a(n) = sum of digits of all previous terms | download | Nile Wymar | |
| A004207 | A004207 beginning at 6666706 | download | Nile Wymar | |
| A004207 | A004207 beginning at 10000000042 | download | Nile Wymar | |
|
| ||||
| A000057 | Primes dividing all Fibonacci sequences. | download | Sherry Chen | |
| A000059 | Numbers n such that (2n)^4 + 1 is prime. | download | Sherry Chen | |
| A000062 | A Beatty sequence: a(n) = floor(n/(e-2)). | download | Sherry Chen | |
| A000068 | Numbers n such that n^4 + 1 is prime. | download | Sherry Chen | |
| A000069 | Odious numbers: numbers with an odd number of 1's in their binary expansion. | download | Sherry Chen | |
| A000099 | Let A(n) = #{(i,j): i^2 + j^2 <= n}, V(n) = Pi*n, P(n) = A(n) - V(n); sequence gives values of n where |P(n)| sets a new record. | download | Sherry Chen | |
| A000123 | Number of binary partitions: number of partitions of 2n into powers of 2. | download | Sherry Chen | |
| A000124 | Central polygonal numbers (the Lazy Caterer's sequence): n(n+1)/2 + 1; or, maximal number of pieces formed when slicing a pancake with n cuts. | download | Sherry Chen | |
| A000125 | Cake numbers: maximal number of pieces resulting from n planar cuts through a cube (or cake): C(n+1,3)+n+1. | download | Sherry Chen | |
| A034048 | Numbers with multiplicative digital root = 0. | download | Sherry Chen | |
| A277061 | Numbers with multiplicative digital root > 0. | download | Sherry Chen | |
| A227510 | Numbers such that product of digits of n is positive and a substring of n. | download | Sherry Chen | |
| A236402 | Numbers with property that the sum of any pair of adjacent digits is a substring of the number. | download | Sherry Chen | |
| A254621 | Zerofree numbers having product of digits less than or equal to sum of digits | download | Sherry Chen | |
| A062996 | Sum of digits is greater than or equal to product of digits. | download | Sherry Chen | |
|
| ||||
| A000977 | Numbers that are divisible by at least three different primes. | download | Robert Pedersen | |
| A002971 | Numbers k such that 4*k^2 + 25 is prime. | download | Robert Pedersen | |
| A003151 | Beatty sequence for 1+sqrt(2); a(n) = floor(n*(1+sqrt(2))). | download | Robert Pedersen | |
| A003152 | A Beatty sequence: a(n) = floor(n*(1+1/sqrt(2))). | download | Robert Pedersen | |
| A003153 | a(n) = integer nearest n*(1+sqrt(2)). | download | Robert Pedersen | |
| A005100 | Deficient numbers: numbers n such that sigma(n) < 2n. | download | Robert Pedersen | |
| A005101 | Abundant numbers (sum of divisors of n exceeds 2n). | download | Robert Pedersen | |
| A005574 | Numbers k such that k^2 + 1 is prime. | download | Robert Pedersen | |
| A022843 | Beatty sequence for e: a(n) = floor(n*e). | download | Robert Pedersen | |
| A080081 | Beatty sequence for (3+sqrt(13))/2. | download | Robert Pedersen | |
| A022839 | Beatty sequence for sqrt(5). | download | Robert Pedersen | |
| A007304 | Sphenic numbers: products of 3 distinct primes. | download | Robert Pedersen | |
| A007064 | Numbers not of form "nearest integer to n*tau", tau=(1+sqrt(5))/2. | download | Robert Pedersen | |
| A110117 | Beatty sequence for sqrt(2) + sqrt(3). | download | Robert Pedersen | |
| 3 seconds each of Beatty sequences for sqrt(2),sqrt(3),sqrt(5),sqrt(6), sqrt(7) | download | Robert Pedersen | ||
| 1 seconds each of Beatty-like sequences based on c.f. convergents of sqrt(5) | download | Robert Pedersen |