WXML Spring 2019
Number Theory and Noise
Mrigank Arora, Miranda Bugarin, Aanya Khaira
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
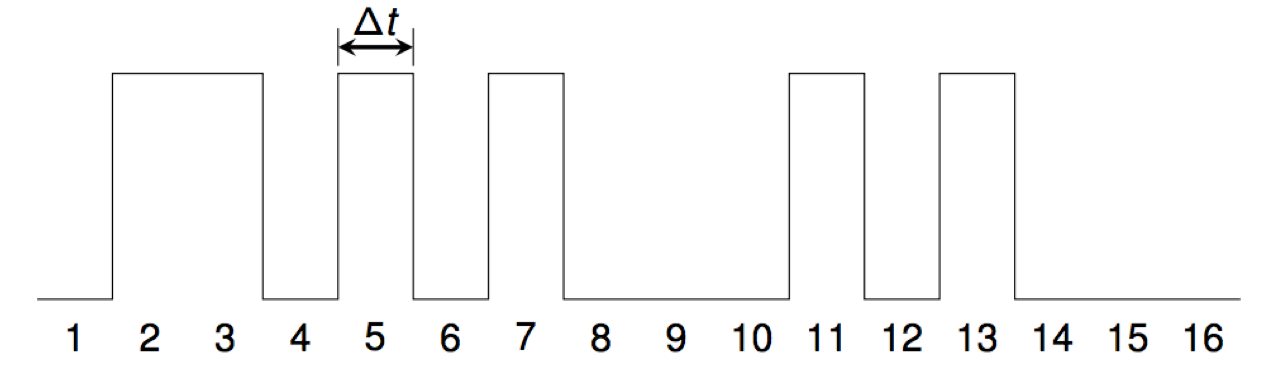
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | download | creator | quarter | tags | comments |
|---|---|---|---|---|---|---|---|
| A005101 | Abundant numbers | download | Mrigank Arora | Spr2019 | |||
| A005101 | Abundant numbers waveform built up from distinct subsequences. | download | Mrigank Arora | Spr2019 | |||
| A091191 | Primitive abundant numbers: abundant numbers having no abundant proper divisor. | download | Mrigank Arora | Spr2019 | |||
| A028374 | Curved numbers: numbers that only have curved digits (0,2,3,5,6,8,9) | download | Mrigank Arora | Spr2019 | digits | ||
| A034470 | Prime numbers using only the curved digits (0,2,3,5,6,8,9) | download | Mrigank Arora | Spr2019 | digits | ||
| A192869 | Thin primes: odd primes p such that p+1 is a prime (or 1) times a power of two. | download | Mrigank Arora | Spr2019 | |||
| A003234 | Numbers n such that A003231(A001950(n)) = A001950(A003231(n)) - 1. | download | Miranda Bugarin | Spr2019 | |||
| A005384 | Sophie Germain primes p: 2p+1 is also prime. | download | Miranda Bugarin | Spr2019 | |||
| A007640 | Numbers k such that 2*k^2 - 2*k + 19 is composite. | download | Miranda Bugarin | Spr2019 | |||
| A055471 | Divisible by the product of its nonzero digits. | download | Miranda Bugarin | Spr2019 | digits | ||
| A071204 | Numbers which are multiples of their largest decimal digit. | download | Miranda Bugarin | Spr2019 | digits | ||
| A052382 | Numbers without 0 as a base 10 digit, a.k.a. zeroless numbers. | download | Miranda Bugarin | Spr2019 | digits | ||
| A082943 | Numbers without zero digits that are not divisible by any of their digits nor by the sum of their digits. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031956 | Numbers in which the number of distinct base 4 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031957 | Numbers in which the number of distinct base 5 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031958 | Numbers in which the number of distinct base 6 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031959 | Numbers in which the number of distinct base 7 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031960 | Numbers in which the number of distinct base 8 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031961 | Numbers in which the number of distinct base 9 digits is 3. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031962 | Numbers with exactly two distinct base 10 digits. | download | Miranda Bugarin | Spr2019 | digits | ||
| A031955 | Numbers with exactly two distinct base 10 digits. | download | Miranda Bugarin | Spr2019 | digits | ||
| A101594 | Numbers with exactly two distinct decimal digits, neither of which is 0. | download | Miranda Bugarin | Spr2019 | digits | ||
| A155107 | Numbers n that are 23 or 30 (mod 53). | download | Miranda Bugarin | Spr2019 | |||
| A000404 | Numbers that are the sum of 2 nonzero squares. | download | Aanya Khaira | Spr2019 | |||
| A000443 | Numbers that are the sum of 2 squares in exactly 3 ways. | download | Aanya Khaira | Spr2019 | |||
| A025284 | Numbers that are the sum of 2 nonzero squares in exactly 1 way. | download | Aanya Khaira | Spr2019 | |||
| A025285 | Numbers that are the sum of 2 nonzero squares in exactly 2 ways. | download | Aanya Khaira | Spr2019 | |||
| A025286 | Numbers that are the sum of 2 nonzero squares in exactly 3 ways. | download | Aanya Khaira | Spr2019 | |||
| A025287 | Numbers that are the sum of 2 nonzero squares in exactly 4 ways. | download | Aanya Khaira | Spr2019 | |||
| A002620 | Quarter-squares: floor(n/2)*ceiling(n/2). Equivalently, floor(n^2/4). | download | Aanya Khaira | Spr2019 | |||
| A scale played on a piano. | download | Aanya Khaira | Spr2019 | ||||
| The sound file above converted into an integer sequence then converted back to sound. | download | Aanya Khaira | Spr2019 | ||||
| A voice saying a few words. | download | Aanya Khaira | Spr2019 | ||||
| The sound file above converted to an integer sequences then converted back to sound. | download | Aanya Khaira | Spr2019 | ||||
| A000408 | Numbers that are the sum of three nonzero squares. | download | Aanya Khaira | Spr2019 | |||
| A025324 | Numbers that are the sum of 3 nonzero squares in exactly 4 ways | download | Aanya Khaira | Spr2019 | |||
| A025325 | Numbers that are the sum of 3 nonzero squares in exactly 5 ways | download | Aanya Khaira | Spr2019 | |||
| A025326 | Numbers that are the sum of 3 nonzero squares in exactly 6 ways | download | Aanya Khaira | Spr2019 | |||
| A025327 | Numbers that are the sum of 3 nonzero squares in exactly 7 ways | download | Aanya Khaira | Spr2019 | |||
| A025328 | Numbers that are the sum of 3 nonzero squares in exactly 8 ways | download | Aanya Khaira | Spr2019 | |||
| A025329 | Numbers that are the sum of 3 nonzero squares in exactly 9 ways | download | Aanya Khaira | Spr2019 | |||
| A025330 | Numbers that are the sum of 3 nonzero squares in exactly 10 ways | download | Aanya Khaira | Spr2019 | |||
| A000408 | Numbers that are the sum of 3 nonzero squares in exactly n ways where n is increasing geometrically by doubling every 2.2 seconds. | download | Aanya Khaira | Spr2019 |