WXML Winter 2018
Number Theory and Noise
Sherry Chen, Joo Young "Jon" Kim, Joshua Ramirez
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
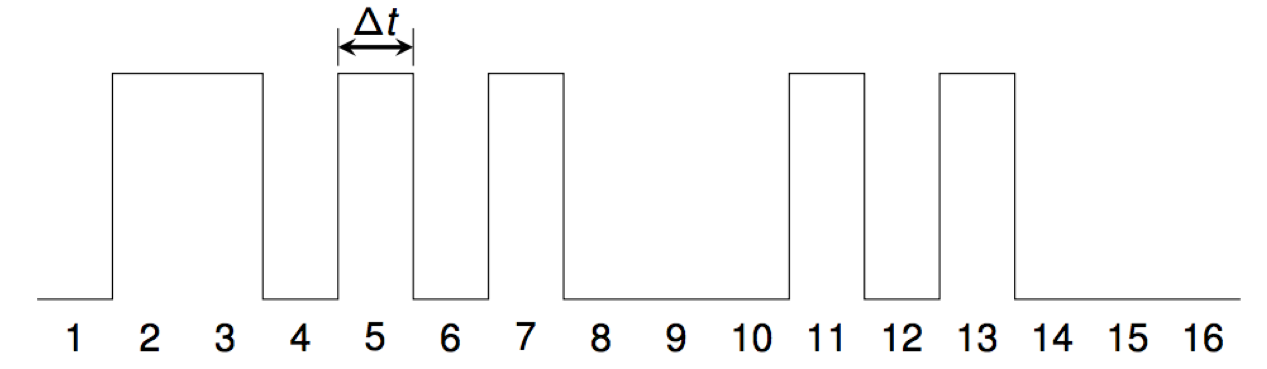
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | creator | |
| A001913 | Full reptend primes: primes with primitive root 10. | download | Joo Young "Jon" Kim | |
| A001504 | a(n) = (3n+1)(3n+2). | download | Joo Young "Jon" Kim | |
| Numbers congruent to 4 or 7 mod 87 | download | Joo Young "Jon" Kim | ||
| Number congruent to 0 mod 51 | download | Joo Young "Jon" Kim | ||
| Previous waveform approximated by an increasing number of terms of its Fourier series up to the Nyquist frequency | download | Joo Young "Jon" Kim | ||
| A014261 | Numbers that contain odd digits only. | download | Sherry Chen | |
| A059708 | Numbers n such that all digits have same parity. | download | Sherry Chen | |
| A267085 | Numbers such that the number formed by digits in even position divides, or is divisible by, the number formed by the digits in odd position; both must be nonzero. | download | Sherry Chen | |
| A267086 | Numbers such that the number formed by digits in even positions divides, or is divisible by, the number formed by the digits in odd positions; zero allowed. (terms up to 5x106) | download | Sherry Chen | |
| A267086 | Numbers such that the number formed by digits in even positions divides, or is divisible by, the number formed by the digits in odd positions; zero allowed. (terms between 1010 and 1010+5x106 ) | download | Sherry Chen | |
| A236402 | Numbers with property that the sum of any pair of adjacent digits is a substring of the number. | download | Sherry Chen | |
| A236402-21fact | Numbers with property that the sum of any pair of adjacent digits is a substring of the number (sequence starting from 21!) | download | Sherry Chen | |
| A007304 | Sphenic numbers: products of 3 distinct primes. | download | Joshua Ramirez | |
| A023204 | Numbers m such that m and 2*m + 3 are both prime. | download | Joshua Ramirez | |
| A007602 | Numbers that are divisible by the product of their digits. | download | Joshua Ramirez | |
| A039770 | Numbers n such that phi(n) is a perfect square. | download | Joshua Ramirez | |
| A006532 | Numbers n such that sum of divisors of n is a square. | download | Joshua Ramirez | |
| A276967 | Odd integers n such that 2^n == 2^3 (mod n). | download | Joshua Ramirez | |
| A003624 | Duffinian numbers: n composite and relatively prime to sigma(n). | download | Joshua Ramirez | |
| A015765 | Numbers n such that phi(n) | sigma_7(n). | download | Joshua Ramirez | |
| A005835 | Pseudoperfect (or semiperfect) numbers n: some subset of the proper divisors of n sums to n. | download | Joshua Ramirez | |
| A007675 | Numbers n such that n, n+1 and n+2 are squarefree. | download | Joshua Ramirez | |
| A001122 | Primes with primitive root 2. | download | Joshua Ramirez | |
| A057531 | Numbers n such that sum of digits of n equals the numbers of divisors of n. | download | Joshua Ramirez | |
| A152088 | Positive integers n that when written in binary have exactly the same number of (non-leading) 0's as the number of divisors of n. | download | Joshua Ramirez | |
| A110806 | Numbers n such that sum of the digits as well as number of digits divides n. | download | Joshua Ramirez | |
| A023172 | Self-Fibonacci numbers: numbers n such that n divides Fibonacci(n). | download | Joshua Ramirez | |
| A001837 | Numbers n such that phi(2n+1) < phi(2n). | download | Joshua Ramirez |