WXML Spring 2017

Number Theory and Noise

Penny Espinoza, Emily Flanagan, Hannah Van Wyk

This project investigates the representations of sets of positive integers (sequences) as sound.

A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.

For example, the waveform for the primes starts like this:



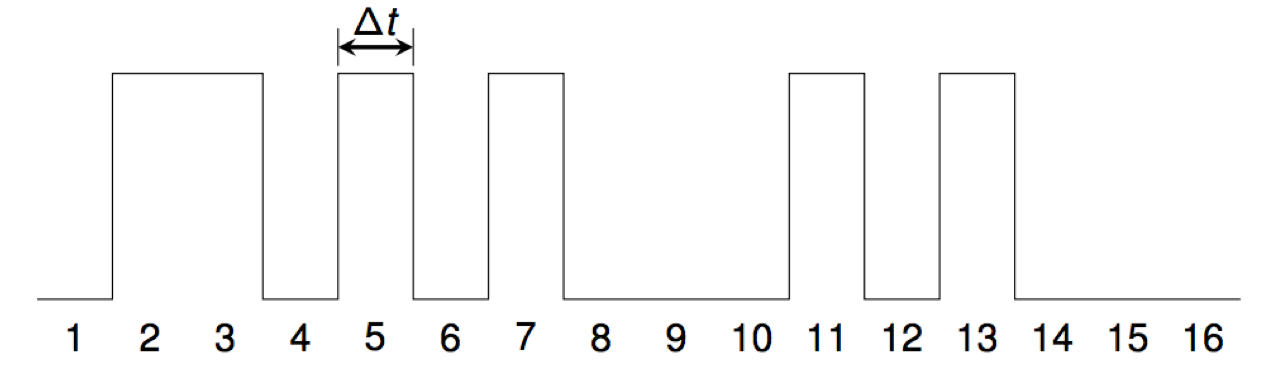
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.

For many sets, the result is what most people would describe as noise.

Special

description sound player creator
rational convergents toward sqrt(2) Beatty sequencedownloadEmily Flanagan
composites with progressively increasing maximal prime factor (2-19), then all compositesdownloadPenny Espinoza


OEIS sequences

OIES iddescription sound player creator
A184774 primes of the form floor(k*sqrt(2))downloadEmily Flanagan
A184775 numbers n such that floor(n*sqrt(2)) is prime downloadEmily Flanagan
A184777 primes of the form 2k + floor(k*sqrt(2))downloadEmily Flanagan
A184778 numbers n such that 2n+floor(n*sqrt(2)) is prime downloadEmily Flanagan
A002984 a(0) = 1; for n>0, a(n) = a(n-1) + floor( sqrt a(n-1) ) downloadEmily Flanagan
A013929 non-squarefree numbersdownloadEmily Flanagan
A017533number of the form 12n+1 downloadEmily Flanagan
A158708 primes p such that p + floor(p/2) is primedownloadEmily Flanagan
A158709 primes p such that p + ceiling(p/2) is primedownloadEmily Flanagan
A168363 squares and cubes of primesdownloadEmily Flanagan
A175914 primes p such that p+2*q is prime, where q is the prime after pdownloadEmily Flanagan
A000093 a(n) = floor(n^(3/2)).downloadEmily Flanagan
A000212 a(n) = floor(n^2/3) downloadEmily Flanagan
A001952a Beatty sequence: a(n) = floor(n*(2 + sqrt(2))) downloadEmily Flanagan
A002620quarter-squares: floor(n/2)*ceiling(n/2), equivalently, floor(n^2/4) downloadEmily Flanagan
A003154centered 12-gonal numbers (also star numbers: 6*n*(n-1) + 1). downloadEmily Flanagan
A007590floor(n^2/2) downloadEmily Flanagan
A014657 numbers n that divide 2^k + 1 for some kdownloadEmily Flanagan
A032528concentric hexagonal numbers: floor( 3*n^2 / 2 ) downloadEmily Flanagan
A033581 a(n) = 6*n^2 downloadEmily Flanagan
A035336 a(n) = 2*floor(n*phi) + n - 1, where phi = (1+sqrt(5))/2 downloadEmily Flanagan
A072065 numbers of the form 12n+k, where k=0, 2, 9, or 11 downloadPenny Espinoza
A000040the primes, starting from 1 downloadPenny Espinoza
A000040the primes, starting from 107 downloadPenny Espinoza
A000040the primes, starting from 108 downloadPenny Espinoza
A000040 the primes, starting from 109downloadPenny Espinoza
A000040the primes, starting from 1010 downloadPenny Espinoza
A000040 the primes, starting from 1011downloadPenny Espinoza
A000040the primes, starting from 1012 downloadPenny Espinoza
A000040primes, starting at 1010 downloadPenny Espinoza
A000040primes, starting at 1020 downloadPenny Espinoza
A000040primes, starting at 1030 downloadPenny Espinoza
A000040primes, starting at 1040 downloadPenny Espinoza
A000040primes, starting at 10100 downloadPenny Espinoza
A000040primes, starting at 10200 downloadPenny Espinoza
A000040 primes, starting at 10400 downloadPenny Espinoza
A077800twin primes, starting at 1010 downloadPenny Espinoza
A077800twin primes, starting at 1030downloadPenny Espinoza
A077800twin primes, starting at 10100downloadPenny Espinoza
A050504floor of n log n downloadHannah Claire Van Wyk
floor of n^1.01 downloadHannah Claire Van Wyk

Spectrograms

back to integer sequence noise page