WXML Autumn 2018
Number Theory and Noise
Joo Young "Jon" Kim, Erik Huang, Pooja Ramanathan
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
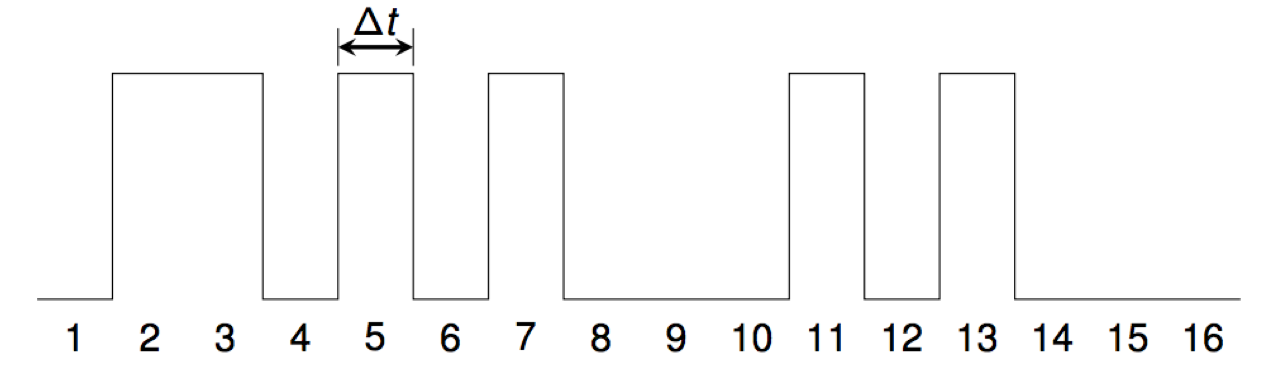
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | download | creator | quarter | tags | comments |
|---|---|---|---|---|---|---|---|
| A000069 | Odious numbers: numbers with an odd number of 1's in their binary expansion. | download | Erik Huang | Aut2018 | |||
| A000290 | The squares | download | Erik Huang | Aut2018 | |||
| A000567 | Octagonal numbers: n*(3*n-2). Also called star numbers. | download | Erik Huang | Aut2018 | |||
| A000959 | Lucky numbers | download | Erik Huang | Aut2018 | |||
| A001105 | a(n) = 2*n^2. | download | Erik Huang | Aut2018 | |||
| A001964 | Wythoff game. | download | Erik Huang | Aut2018 | |||
| A002061 | Central polygonal numbers: a(n) = n^2 - n + 1. | download | Erik Huang | Aut2018 | |||
| A002113 | Palindromes in base 10. | download | Erik Huang | Aut2018 | |||
| A002808 | The composite numbers: numbers n of the form x*y for x > 1 and y > 1. | download | Erik Huang | Aut2018 | |||
| A006753 | Smith numbers: composite numbers n such that sum of digits of n = sum of digits of prime factors of n (counted with multiplicity). | download | Erik Huang | Aut2018 | |||
| A006995 | Binary palindromes: numbers whose binary expansion is palindromic. | download | Erik Huang | Aut2018 | |||
| A007602 | Numbers that are divisible by the product of their digits. | download | Erik Huang | Aut2018 | |||
| A007623 | Integers written in factorial base. | download | Erik Huang | Aut2018 | |||
| A007770 | Happy numbers: numbers whose trajectory under iteration of sum of squares of digits map includes 1. | download | Erik Huang | Aut2018 | |||
| A010784 | Numbers with distinct decimal digits. | download | Erik Huang | Aut2018 | |||
| A014190 | Palindromes in base 3 (written in base 10). | download | Erik Huang | Aut2018 | |||
| A014192 | Palindromes in base 4 (written in base 10). | download | Erik Huang | Aut2018 | |||
| A014486 | List of totally balanced sequences of 2n binary digits written in base 10. Binary expansion of each term contains n 0's and n 1's and reading from left to right (the most significant to the least significant bit), the number of 0's never exceeds the number of 1's. | download | Erik Huang | Aut2018 | |||
| A018252 | The nonprime numbers (1 together with the composite numbers). | download | Erik Huang | Aut2018 | |||
| A029803 | Numbers that are palindromic in base 8. | download | Erik Huang | Aut2018 | |||
| A029952 | Palindromic in base 5. | download | Erik Huang | Aut2018 | |||
| A029953 | Palindromic in base 6. | download | Erik Huang | Aut2018 | |||
| A029954 | Palindromic in base 7. | download | Erik Huang | Aut2018 | |||
| A029955 | Palindromic in base 9. | download | Erik Huang | Aut2018 | |||
| A050224 | 1/2-Smith numbers. | download | Erik Huang | Aut2018 | |||
| A052223 | Numbers whose sum of digits is 9. | download | Erik Huang | Aut2018 | |||
| A072543 | Numbers whose largest decimal digit is also the initial digit (to 107) | download | Erik Huang | Aut2018 | |||
| A104390 | 2-Smith numbers. | download | Erik Huang | Aut2018 | |||
| A139250 | Toothpick sequence. | download | Erik Huang | Aut2018 | |||
| A153880 | Shift factorial base representation left by one digit (to 4 million) | download | Erik Huang | Aut2018 | |||
| A166459 | Numbers whose sum of digits is 19. | download | Erik Huang | Aut2018 | |||
| A235151 | Numbers whose sum of digits is 12. | download | Erik Huang | Aut2018 | |||
| A235229 | Numbers whose sum of digits is 20. | download | Erik Huang | Aut2018 | |||
| A243615 | Numbers n whose digital sum equals the number of binary digits in its binary expansion. | download | Erik Huang | Aut2018 | |||
| A243617 | Numbers n whose sum of digits equals the number of bits in its binary expansion. No zeros allowed in the digital expansion. | download | Erik Huang | Aut2018 | |||
| A001358 | Semiprimes | download | Pooja Ramathan | Aut2018 | |||
| A003622 | The Wythoff compound sequence AA: [n*phi^2] - 1, where phi = (1+sqrt(5))/2. | download | Pooja Ramathan | Aut2018 | beatty | ||
| A004678 | Primes written in base 4. | download | Pooja Ramathan | Aut2018 | |||
| A004680 | Primes written in base 6. | download | Pooja Ramathan | Aut2018 | |||
| A004754 | Numbers whose binary expansion starts 10. | download | Pooja Ramathan | Aut2018 | |||
| A004758 | Binary expansion starts 110. | download | Pooja Ramathan | Aut2018 | |||
| A005728 | Number of fractions in Farey series of order n. | download | Pooja Ramathan | Aut2018 | |||
| A005891 | Centered pentagonal numbers: (5n^2+5n+2)/2. | download | Pooja Ramathan | Aut2018 | |||
| A005994 | Alkane (or paraffin) numbers l(7,n). | download | Pooja Ramathan | Aut2018 | |||
| A100484 | Even semiprimes | download | Pooja Ramathan | Aut2018 | |||
| A112393 | Semiprimes n such that 3*n - 2 is a square. | download | Pooja Ramathan | Aut2018 | |||
| A242756 | Semiprimes having only the curved digits. | download | Pooja Ramathan | Aut2018 | |||
| A277093 | Numbers k such that sin(k) > 0 and sin(k+2) > 0. | download | Pooja Ramathan | Aut2018 | |||
| Approximation of A277093 based on difference pattern [6,6,6,7,6,6,6,1] | download | Pooja Ramathan | Aut2018 | ||||
| Approximation of A277093 based on difference pattern [6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7,6,6,6,1,6,6,6,7] | download | Pooja Ramathan | Aut2018 | ||||
| A277094 | Numbers k such that sin(k) > 0 and sin(k+2) < 0. | download | Pooja Ramathan | Aut2018 | |||
| A277095 | Numbers k such that sin(k) < 0 and sin(k+2) > 0. | download | Pooja Ramathan | Aut2018 | |||
| A277096 | Numbers k such that sin(k) < 0 and sin(k+2) < 0. | download | Pooja Ramathan | Aut2018 | |||
| Numbers n congruent to 0 mod 1000. | download | Joo Young "Jon" Kim | Aut2018 | ||||
| Numbers n congruent to 1 mod 1000. | download | Joo Young "Jon" Kim | Aut2018 | ||||
| Numbers n congruent to 479 mod 1000. | download | Joo Young "Jon" Kim | Aut2018 | ||||
| Numbers congurnet to 0 or n mod 30, with n running from 0 to 30, increasing each second. | download | Joo Young "Jon" Kim | Aut2018 |