WXML Autumn 2017
Number Theory and Noise
Nile Wymar, Lisa Yan
This project investigates the representations of sets of positive integers (sequences) as sound.
A digital audio waveform is created from a given set A of positive integers by setting sample number i to a non-zero constant c for all i in the set. All other samples are set to zero.
For example, the waveform for the primes starts like this:
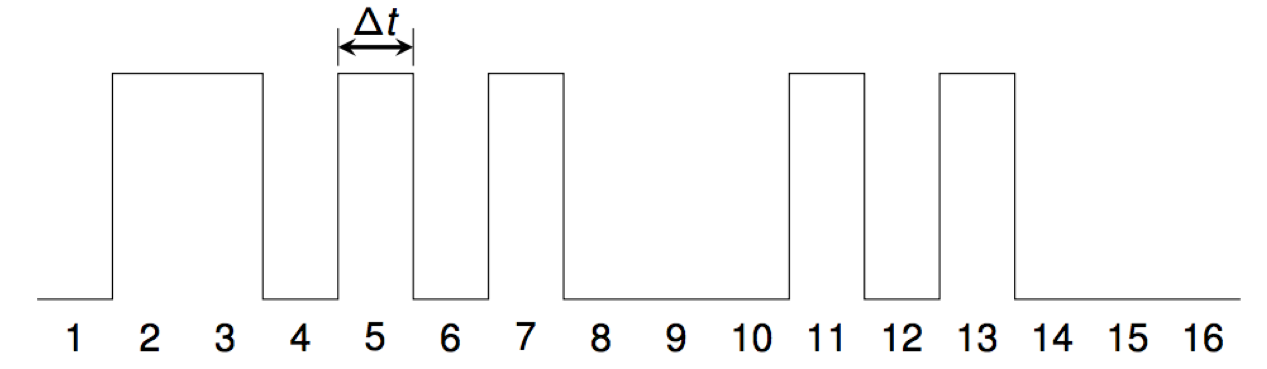
We use the standard CD-audio sampling rate of 44100 samples per second, so Δt = 1/44100= 0.0000226757... seconds.
For many sets, the result is what most people would describe as noise.
OEIS sequences
| OIES id | description | sound player | creator | |
| A050504 | Floor of n log n | download | Hannah Claire Van Wyk | |
| A000059 | Numbers n such that (2n)^4 + 1 is prime. | download | Nile Wymar | |
| A000068 | Numbers n such that n^4 + 1 is prime. | download | Nile Wymar | |
| A000469 | 1 together with products of 2 or more distinct primes | download | Nile Wymar | |
| A000879 | Number of primes < prime(n)^2 | download | Nile Wymar | |
| A001043 | Numbers that are the sum of 2 successive primes | download | Nile Wymar | |
| A000062 | a(n) = floor(n/(e-2)). | download | Nile Wymar | |
| A000572 | a(n)= floor (n(e+1)) | download | Nile Wymar | |
| A000201 | a(n) = floor(n*phi), where phi = (1+sqrt(5))/2 | download | Nile Wymar | |
| A000277 | 3*n - 2*floor(sqrt(4*n+5)) + 5 | download | Nile Wymar | |
| A001097 | Twin primes | download | Nile Wymar | |
| A005101 | Abundant numbers (sum of divisors of n exceeds 2n) | download | Nile Wymar | |
| A005100 | Deficient numbers: numbers n such that sigma(n) < 2n. | download | Nile Wymar | |
| A007066 | a(n) = 1 + ceiling((n-1)*phi^2), phi = (1+sqrt(5))/2. | download | Nile Wymar | |
| A007510 | Single (or isolated or non-twin) primes: Primes p such that neither p-2 nor p+2 is prime | download | Nile Wymar | |
| A007645 | Generalized cuban primes: primes of the form x^2 + xy + y^2; or primes of the form x^2 + 3*y^2; or primes == 0 or 1 mod 3. | download | Nile Wymar | |
| A030059 | Numbers that are the product of an odd number of distinct primes | download | Nile Wymar | |
| A001951 | Beatty sequence: floor(sqrt(2)n) | download | ||
| Beatty sequence for 1.4 | download | |||
| Beatty sequence for 1.41 | download | |||
| Beatty sequence for 1.414 | download | |||
| Beatty sequence for 1.4142 | download | |||
| A047381 | floor(n*7/5) | download | Lisa Yan | |
| floor(n*577/408) | Lisa Yan | |||
| A001950 | floor(n*phi^2) | download | Lisa Yan | |
| A003152 | floor(n*(1+1/sqrt(2))) | download | Lisa Yan | |
| A003511 | floor( n * (1 + sqrt(3))/2 ) | download | Lisa Yan | |
| A059535 | floor( n * Pi^2/6 ) | download | Lisa Yan | |
| A022844 | floor( n * Pi ) | download | Lisa Yan | |
| A028834 | Numbers n such that the sum of digits of n is a prime. | download | Nile Wymar | |
| A028838 | Numbers n such that the sum of digits of n is a power of 2 | download | Nile Wymar | |
| A028839 | Number n such that the sum of digits of n is a square | download | Nile Wymar | |
| A028840 | Numbers n such that the sum of digits of n is a Fibonacci number | download | Nile Wymar | |
| A054683 | Numbers n such that the sum of digits is even | download | Nile Wymar | |
| A295389 | Numbers n such that the sum of digits is square-free | download | Nile Wymar | |
| A061910 | Numbers n such that the sum of digits of n^2 is a square | download | Nile Wymar | |
| Base 2 version of A61910: n such that sum of binary digits of n^2 is square | download | Nile Wymar | ||
| A237525 | Numberd n such that the sum of digits of n^3 is a cube | download | Nile Wymar | |
| A235227 | Numbers n such that the sum of digits is 16 | download | Nile Wymar | |
| Numbers n such that sum of digits is 25 | download | Nile Wymar | ||
| Numbers n such that sum of digits is 36 | download | Nile Wymar | ||
| A084561 | Sum of binary digits is a square | download | Nile Wymar | |
| A001969 | Sum of binary digits is even | download | Nile Wymar |