June 8, 2018
Statistics for the final exam: n=109; min=2; 1st quartile=24; median=43; 3rd quartile=53; max=69.
Here is a histogram of scores on the final exam.

May 30, 2018
Here is an example showing the use of a sinusoidal function compared to a "linear" (really, "sawtooth" would be a better description) function in creating animations.
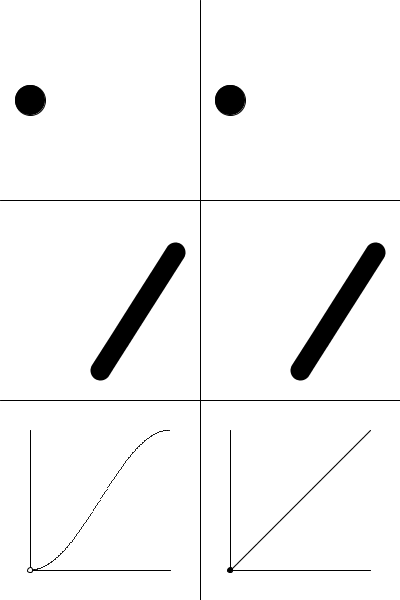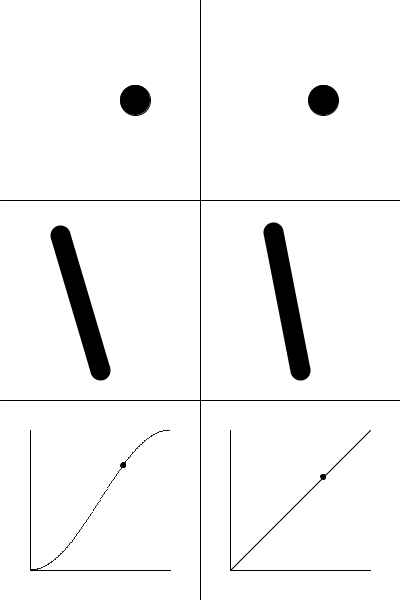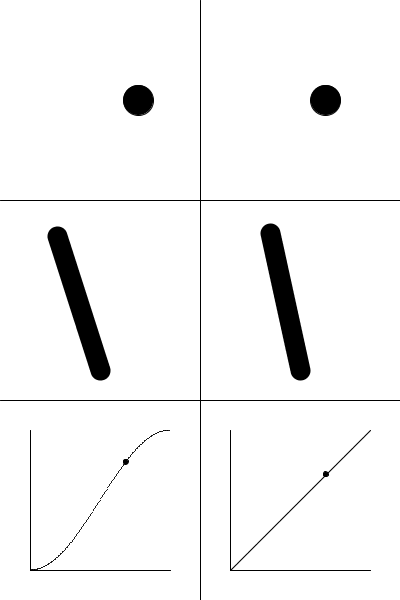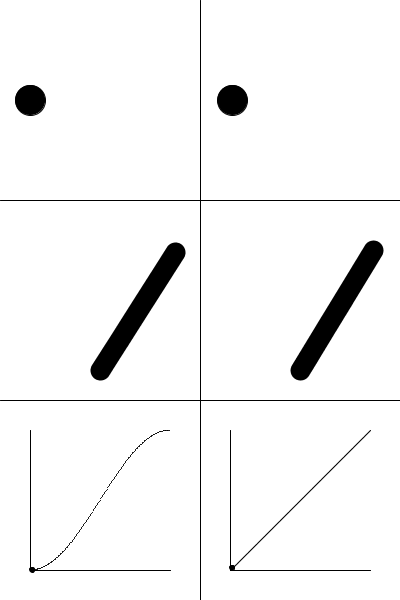
May 29,2018
To help you study for the final exam, here is a review sheet, and a list of some of the mechanical skills you will want to have well honed.
Comments on sinusoidal function work:
- We continued our example of the temperature in the desert. This led us to the problem of solving an equation of the form f(t)=k, where f is a sinusoidal function. This led to...
- Inverse Sine Since sin x is not one-to-one it has no inverse. However, we can restrict sin x to a piece of its domain on which it is one-to-one, and then that function has an inverse. By restricting sin x to the interval -pi/2 ≤ x ≤ pi/2, we get a function with an inverse; that function is known as arcsine or the inverse sine, written sin-1 x. This function has domain -1 ≤ x ≤ 1 and range -pi/2 ≤ y <e; pi/2. Thus we can graph the entire function! Notice that this is unlike any other function we've seen: all other functions have an infinite domain and/or an infinite range. Inverse sine has finite domain and finite range.
- We can use the inverse sine to solve equations involving sinusoidal functions, but the key thing to remember is that the inverse sine will only give us one solution: if a sinusoidal equation as any solutions, then it has infinitely many. Fortunately, we can utilize the symmetry and periodicity of the graph of sinusoidal functions to find all the other solutions, once we know one of them.
- We can the first solution we get by applying the inverse sine the principal solution. This will always be the solution nearest to the value of C: on the half-period around t=C, the function will be increasing, just the way that sin x is increasing from x=-pi/2 to x=pi/2. As a result, this is where you will find the solution given via inverse sine. Then, we can find the symmetry solution by utilizing the symmetry of the graph around the maximal points (peaks). If T is the time at the maximum to the right of C, and P is the principal solution, then the symmetry solution S can be found to be S = T+(T-P): the symmetry solution is the same amount to the right of the maximum that the principal solution was to the left.
- Once we have the principal solution P and the symmetry solution S, all solutions can be expressed in the form P+Bk or S+Bk, where B is the period, and k is an integer (0, ±1, ±2, etc.). We can use this to generate as many solutions as we need to solve the given problem.
May 21, 2018
Midterm two statistics: n=118; min= 0; 1st quartile=15; median=25; 3rd quartile=32; max=40 (4 students).
Here is a histogram of midterm two scores.

May 13, 2018
NOTE: There will be no quiz section on Tuesday, May 15, due to a strike by at least some graduate student workers.
Midterm is Thursday, May 17. It will cover topics in Chapters 8 through 16. Here is a review sheet of the mechanical aspects of these topics.
When looking at old exams on the exam archive, keep in mind that some exams may cover topics in chapter 17, or chapter 7, which you will not be responsible for on your exam.
Here are some specific suggestions about old exams.
- Spring 2017, all problems are worth studying.
- Winter 2017, problems 2, 3, and 4 are worth studying.
- Autumn 2014, problems 1, 3, and 4.
- Autumn 2013, problems 1, 2, and 4.
- Spring 2013, problems 1, 3, and 4.
- Winter 2013, problems 2, 3, and 4.
- Autumn 2012, problems 2, 3, and 4.
Please see below on this page (April 11, 2018) for my suggestions for how to study for exams. in this course.
April 25,2018
Petition forms for alternatives to the common final are available in the Mathematics Advising Office, C-36 Padelford (campus map) or online as a PDF, and should be filed by Friday, May 4 at 4:00 pm. You can read more here.
April 24, 2018
Here is plot of data from Math 120 A, Spring 2017. It shows course grade vs midterm one score. As you can see, a low score on the first midterm usually results in a quite low course grade. This plot does not include people who got a low score on the first midterm and then dropped the course.

April 24, 2018
Here is a scatter plot of midterm one scores versus total webassign homework scores (through chapter 7). It is interesting to note that, while having a high homework score appears not to be sufficient to do well on the midterm, it does appear to be more-or-less necessary.

April 23, 2018
First midterm exam statistics: n=127; min=0; 1st quartile=12; median=20; 3rd quartile =28; max=40 (1 student).
Here is a histogram of midterm one scores.

Here is a table of score-to-4.0-scale conversions. This is only to give you a rough idea of how you did on the exam: I do not use these converted values for any purpose.
| ≤13 | 0.0 |
| 14 | 0.7 |
| 15 | 1.0 |
| 16 | 1.3 |
| 17 | 1.7 |
| 18 | 2.0 |
| 19 | 2.4 |
| 20 | 2.7 |
| 21 | 2.8 |
| 22 | 2.9 |
| 23 | 3.0 |
| 24 | 3.0 |
| 25 | 3.1 |
| 26 | 3.2 |
| 27 | 3.3 |
| 28 | 3.4 |
| 29 | 3.5 |
| 30 | 3.5 |
| 31 | 3.6 |
| 32 | 3.7 |
| 33 | 3.8 |
| 34 | 3.9 |
| 35 | 4.0 |
| 36 | 4.0 |
| 37 | 4.0 |
| 38 | 4.0 |
| 39 | 4.0 |
| 40 | 4.0 |
April 15, 2018
Here is a review sheet covering the mechanical aspects of topics through Chapter 7.
April 14, 2018
One type of problem involving quadratic functions that you want to be able to solve is one in which we are given the value of an unknown quadratic function at three points and are asked to find the function. This is equivalent to knowing three points that the graph of an unknown quadratic function passes through. This is not too hard, but it helps to note that the algebraic steps always take the same form, and this let's us follow a similar process every time. Simply put, you will have three equations in three unknowns (a, b, and c), but subtracting any two of the equations eliminates c and so we can end up with two equations in two unknowns (a and b) very quickly. From there, there is not much keeping us from solving the problem (i.e., finding a, b, and c).
This is all illustrated in the handout Quadratic Function Algebra linked at right.
April 11, 2018
Suggestions for preparing for the midterm exam:
- The exam will cover all material through chapter 7.
- The first step in studying for the midterm exam is to read over all of your lecture notes again. For added benefit, I recommend copying all of your lecture notes again by hand. This will ensure that you have not missed anything, and you have given your mind the time needed to have a chance to absorb the concepts.
- The second step in studying for the midterm is to go over all homework problems again. Make sure that you understand how to solve all of them. It is not enough to note that you did get the problem answered correctly on WebAssign.
- The third step in studying for the midterm is to look at the
exam archive.
I recommend only utilizing midterms that I have written, which you can find
in abundance by clicking on "Conroy" anywhere under "Midterm exams...".
Note that each quarter there are two midterms: the one designated #1 is the
one given around the fourth week, and the one designated #2 is the one
given around the 8th week. So, if you are studying for the first midterm,
you only want to consider ones designated #1.
During the exam you are allowed a single 8.5 inch by 11 inch, two-sided, handwritten sheet of notes: now would be a good time to start making it, so that you can use it as you study, and hence will know what is on it, and you won't waste time during the exam looking for things that are not there. The notesheet cannot be, or contain, a printout or photocopy of anything: it must be written out entirely by hand. Take an 8.5 inch by 11 inch blank piece of paper, and start writing on it with a pen or pencil to create your notesheet. You can always write it out again if it becomes to cluttered.
I recommend taking some of the old exams as exams. By that I mean print one out, find a quite place to work where nobody will bother you, turn off your phone, and see what you can get done in 50 minutes without asking for help or using the internet: the only resource you should use is your notesheet. Ideally, you will see that you can get a lot of work done in 50 minutes, and this will give you confidence going into the actual exam. At the same time, working the exams can help you assess what you know well, and what you don't, and so help you know where to focus your studying. - You may find that you take more time to solve certain problems than you would like to. Though the exams are not written with the intention that they must be worked at extreme speed, there is a definite time limit of 50 minutes. I recommend the following time management strategy during the exam. Start the exam by reading over all problems. Then, give yourself a time limit of 10 minutes for each problem. Start with the problem you think you can get done in the least amount of time. Note the time, and if you find you have worked on it for 10 minutes without finishing it, stop working on that problem, and start working on another problem (of course, if you finish in less than 10 minutes, go on to another problem right away). Continue in this way until you have finished, or at least spent 10 minutes on, each problem. You will then have at least 10 minutes to go back and work more on your unfinished problems, check your work, etc. What this strategy avoids is the issue whereby you spend lots of time on a few problems, and run out of time without having made any attempt on one or two problems. It is better to make a solid 10-minute attempt on all problems than to leave any of the problems blank.
- I very strongly encourage you to find other students to studying with. You might form a "study group", and help each other stay focused and honest about your preparedness. It is easy to convince yourself that you know more than you actually do, and having other people to study with can help you have a truer sense of the work that still needs to be done. At the same time, take confidence from everything that you can do, and help your study mates to do the same, by pointing out their capabilities, especially when you see their confidence flagging. (By the way, the Math Study Center is a good place to meet people who you might form a study group with, and it is a place where your group can meet.)
- Graded exams will be returned at the following quiz section (Tuesday). As the course is graded "on a curve", you will not be able to assess how well you did simply from the raw score that will appear on your exam when it is returned to you. I will post information here about how to interpret your score, so check here for that information after you get your graded exam back.
- As always, be sure to make use of all the resources you have available to succeed in this class. My office hours, your TA's office hours, the Math Study Center, and CLUE are all very highly recommended to you to help you study. If you have questions, the course discussion board is a way to communicate with me such that other students can benefit from our conversation.
April 9, 2018
Comments on today's lecture:
- Pizza problems Problems like the one with a piece of steel that we talked about today are often called
"pizza prpblems" in this course after one of the homework problems. Although these problems
can be approached in a variety of ways, the method illustrated
in class will treat all of them well. The steps can be boiled down to:
- Draw a picture of the 'pizza' on a coordinate system, with the origin at the lower left corner and the x-axis along the lower edge.
- Find the coordinates of all vertices (corners) of the pizza.
- Find the equations of all lines making up the upper edge of the pizza.
- Use the fact that a line equation y=mx+b for a portion of the upper edge tells you the length of the cut at x, so use this length in your calculation of the area of that portion of the pizza. You want a function of x that expresses the area to the left of the cut.
- Do this for each portion of the pizza.
- Combine all expressions into a single multipart rule.
April 3, 2018
CLUE Along with the Math Study Center, CLUE is an excellent resource I encourage all students of Math 120 to take advantage of. CLUE is a late-night drop-in study center on campus, and offers free tutoring for math, chemistry, physics, writing, and a number of other subjects. It is open 7-11pm Sunday through Thursday in the Mary Gates Hall commons. This quarter, CLUE also offers daytime math tutoring in the HUB Commuter & Transfer Commons on Wednesdays from 1-4pm. To learn more about CLUE you can visit CLUE's website.
Also, there will be Math 120 priority drop-in sessions. At a priority drop-in session, each of which will run 7-9pm, a math tutor will be designated to help specifically 120 students. (There will be a whiteboard just for 120 students to put their name on if they need help.) The students will be expected to come with questions; this isn't a formal exam review, but it's meant to give extra support to 120 students before their exams.
These sessions will occur on the following dates:
Tuesday April 17
Tuesday May 8
Wednesday May 16
Thursday May 31
March 27, 2018
Algebraic sophistication: As I mentioned in lecture on Monday, an important thing for students in 120 to work on is what we might call algebraic sophistication. What I mean by this term is going beyond the point of just "getting by" when confronted with algebraic problems. Students need to become adept with their algebra skills, and be able to choose the best approach from a few possible options in their methods. Developing this sophistication will require paying attention to your algebra work and thinking about choices that you make when working problems, and noticing how certain choices lead to better outcomes than others. This is not easy, but it can make all the difference in whether or not a student does well in this course, and in calculus.
As an example of what I mean, every time I teach Math 120 I see students that, when they need to expand an expression like (x+2y)2 will apply the "foil" method, write (x+2y)(x+2y) = x^2+x(2y)+(2y)x+(2y)^2, etc. There is no question that this is correct. However, we encounter such expressions a lot; so often, in fact, that we should learn to use the identity (a+b)2 = a2+2ab+b2. With this, you can quickly expand (x+2y)2 = x2+4xy+4y2. Notice that this is identical to what you get when you "foil", but takes fewer steps and so is faster, but more importantly it is less likely to lead to an error (provided, of course, that you use the identity correctly).
There are many small things like this in our algebra work that can make a big difference in how quickly and how accurately we can solve problems (on exams, in particular, where time is limited, and you don't get multiple attempts as you do with the WebAssign homework). In lecture, I will be illustrating many of these methods: pay particular attention where I use algebra in a way that seems different from the way the you would. I will, as far as I am able, be showing you the shortest, safest, least tedious way to approach the algebra.
March 22, 2018
Welcome to Math 120 A Spring quarter 2018.
Announcements and other useful things will be posted here during the quarter.
Textbook: The textbook for this course is Precalculus, by Collingwood, Prince and Conroy. The book can be purchased at the UW Bookstore.
You do not have to purchase the textbook. It is available electronically: here is a direct link to the pdf.
Reading schedule: I have started a reading schedule (see the link at right) so you can stay on top of course topics, access all additional course materials, and get the most from lectures.
Discussion Board: The course has a discussion board (link at right). This is a great way to ask questions of me in a way that will benefit all students in the course. You can ask about homework questions, studying methods, etc. You can also use it to coordinate study sessions with other students.
Homework: We will be using WebAssign for homework.
WebAssign: You can log in to WebAssign here. This will require your UW Net ID. Your UW Net ID is the part of your university email address before the @ symbol. The password to log in is your UW Net ID password.
You must be enrolled in the course in order to get access to the homework on WebAssign.
You will need to purchase an access code before the grace period ends. You can purchase an access code on the WebAssign website after logging in.
The first homework assignment will be due on the night of April 3.
If you are not enrolled in the course, but are trying to add, you can get started on the homework without WebAssign by working the following problems in the textbook (which is freely available here).
Chapter 1: problems 1-10, 14,15
Chapter 2: 2-7, 10, 12, 13
These problems will have different numbers than the ones you will have on WebAssign, but if you write out solutions for these, it won't be too much trouble to rework them with the WebAssign values.
These problems will cover you through the first homework assignment.
I will periodically be expounding here on aspects of the course, particularly study methods and problem-solving tools.Reading the problem This is an often overlooked key step in problem-solving. Be sure to always read the problem carefully, at least twice through before you begin solving the problem. A great way to fail to solve a problem is to attempt to solve a problem that wasn't asked, so make sure you are solving the problem you are given.
I think this is especially true during exams, where you cannot ask for help, or go away and come back to it the next day. So dedicate the first minute or two of work on each exam problem to reading slowly and carefully to be sure you are solving the right problem.
Introducing time variables We've seen in lecture that if an object is moving horizontally at a constant speed in the plane, then its location can be expressed by (A±vt,B), where (A,B) is the "starting location", v is the speed of the object, and t is the time since the object was at the starting location. That is, we are using t=0 to represent that starting time. The plus-or-minus depends on whether or not the object is moving to the right (minus) or left (plus).
A virtually identical method applies to objects moving vertically.
A common issue when using this method occurs when you have more than one object that don't all start moving at the same time. In such a case, you will need to adjust the expression above, keeping in mind that you want to multiply the speed v by the amount of time that the object has been moving since it was at its starting location. In general, this requires replacing t by t+a or t-a for some value of a depending on the start times of your objects.
Rounding and WebAssign In many problems in WebAssign, there is an instruction to round to a certain number of digits. PLEASE IGNORE THIS INSTRUCTION. Instead, keep all digits given by your calculator and enter all of them into WebAssign. I so often see students enter values like 46.5, get a red X, then enter 46.6, thinking that they have rounded wrong, and getting another red X, because their calculation was not correct. A better approach is to enter the full value you get from your calculator (46.51023923, say). In this example, this would still be marked wrong, but you wouldn't waste a second try messing with rounding. I promise that you will never be marked wrong for putting in "too many" digits.
WebAssign attempts For most problems, you have 5 attempts to enter the correct answer (the exceptions are mutliple choice and true-false questions). You should be very stingy about using these attempts. Do everything you can to check your work and your answer before using even the first attempt! Keep in mind that during exams you only get one attempt, so you want to be in the habit of checking your work yourself, and not just relying on WebAssign to tell you whether you have done things correctly.