Math 120 A - Spring 2017 - Dr. Matthew Conroy

June 8, 2017

Final exam stats: n=136; min=2; 1st quartile=20; median=34; 3rd quartile=45.25; max=70 (1 student).

Here is a histogram of scores.

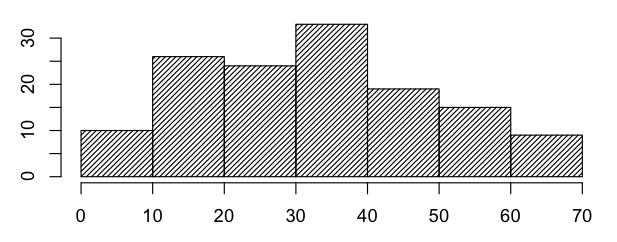
May 26, 2017

To help you study for the final exam, here is a review sheet, and a list of some of the mechanical skills you will want to have well honed.

Comments on today's lecture:

We continued our example of the temperature in the desert. This led us to the problem of solving an equation of the form f(t)=k, where f is a sinusoidal function. This led to...
Inverse Sine Since sin x is not one-to-one it has no inverse. However, we can restrict sin x to a piece of its domain on which it is one-to-one, and then that function has an inverse. By restricting sin x to the interval -pi/2 ≤ x ≤ pi/2, we get a function with an inverse; that function is known as arcsine or the inverse sine, written sin^-1 x. This function has domain -1 ≤ x ≤ 1 and range -pi/2 ≤ y <e; pi/2. Thus we can graph the entire function! Notice that this is unlike any other function we've seen: all other functions have an infinite domain and/or an infinite range. Inverse sine has finite domain and finite range.
We can use the inverse sine to solve equations involving sinusoidal functions, but the key thing to remember is that the inverse sine will only give us one solution: if a sinusoidal equation as any solutions, then it has infinitely many. Fortunately, we can utilize the symmetry and periodicity of the graph of sinusoidal functions to find all the other solutions, once we know one of them.
We can the first solution we get by applying the inverse sine the principal solution. This will always be the solution nearest to the value of C: on the half-period around t=C, the function will be increasing, just the way that sin x is increasing from x=-pi/2 to x=pi/2. As a result, this is where you will find the solution given via inverse sine. Then, we can find the symmetry solution by utilizing the symmetry of the graph around the maximal points (peaks). If T is the time at the maximum to the right of C, and P is the principal solution, then the symmetry solution S can be found to be S = T+(T-P): the symmetry solution is the same amount to the right of the maximum that the principal solution was to the left.
Once we have the principal solution P and the symmetry solution S, all solutions can be expressed in the form P+Bk or S+Bk, where B is the period, and k is an integer (0, ±1, ±2, etc.). We can use this to generate as many solutions as we need to solve the given problem.

May 24, 2017

Comments on Wednesday's lecture:

Sinusoidal functions These are functions of the form f(t)=A sin ( (2pi/B) (t - C) ) + D. where the parameters are:
- A: the amplitude. It is half the vertical distance between the highest and lowest points on the graph of the function. It is the amount that the function deviates from its mean.
- B: the period. This is the horizontal distance between two adjacent peaks (high points) on the graph, or two low points. Half the period is the horizontal distance between a high point and the next low point, or a low point and the next high point. The period is also called the wavelength.
- C: the phase shift. This is the amount the sine function has been shifted away from zero. It can be found by determining where the function is increasing and crossing its mean line. C is not unique: if C is the phase shift, C plus any integer multiple of B will be an equivalent phase shift due to the periodic nature of these functions.
- D: the mean. This is the average value of the function, and is half way between the maximum and minimum values of the function. The graph is perfectly balanced on either side of the line y=D.
In applications, we will need to take information about a sinusoidal function and use that to figure out A, B, C, and D. The first step will always be to sketch the graph based on the information given. If information about less than a full period is given, the graph should be extended to at least a full period.

May 22, 2017

Comments on today's lecture:

We looked at sin x and cos x as functions (just like e^x, or x²+3x+5, etc.). The primary feature that makes sin x and cos x special is their periodicity: they are periodic with period 2 pi. This means that sin(x+ 2 pi) = sin (x) for all x and cos(x+ 2 pi) = cos(x) for all x. This means that the curves y=sin x and y=cos x repeat themselves, and so lend themselves to be useful when modeling repeating phenomena (like waves, for example). Also, it makes it possible to graph y=sin x and y=cos x by graphing them on an interval of length 2 pi (say 0 ≤ x ≤ 2 pi) and then repeating that chunk of the graph indefinitely to the left and right. And that means that we can understand all we need to understand about sin x and cos x if we understand them on 0 ≤ x ≤ 2 pi.
Critically, you should be able to graph y=sin x from the unit circle definition. You should practice this several times, to the point where you really feel the relationship between the unit circle definition and the shape of the graph of sin x.
We briefly talked about tan x, but we won't make use of it. You'll see a lot of it in Math 124. Notably, it has period pi, passes through the origin, and has infinitely many vertical asymptotes.
To make use of sin x, we generalize to the class of sinusoidal functions, which are those functions of the form
f(t)=A sin ( (2pi/B) (t - C) ) + D. These are shifted/scaled versions of y=sin x, so their graphs are shifted and stretched/compressed versions of the graph of sin x. This makes them useful for modeling waves, which are often assumed to have this form (and, in any case, the sinusoidal functions can be used at least as good first approximations of wave-like phenomena).

May 22, 2017

Statistics from the second midterm: n=144; min=1; 1st quartile=15.75; median=24; 3rd quartile = 31; max=40 (2 students)

Here is a histogram of the scores:

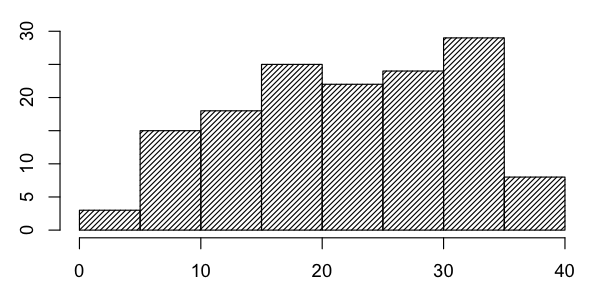
Answers are available on the 120 Materials Website.

Estimated course grades will be posted on Catalyst soon.

May 19, 2017

Comments on today's lecture:

We talked about a general formulation for modeling uniform linear motion: the angular position of an object moving around a circle at constant speed can be given by θ = θ₀ ± ω t where
- θ₀ is the initial angular location (i.e., the angular position at time t=0)
- ω is the angular speed
- The ± choice is determine by the direction of motion: + if counterclockwise, - if clockwise
We can then use (r cos θ, r sin θ) to find the coordinates of the moving object at time t.
To find r when it is not explicitly given, we use v=r ω .
With ferris wheel problems, often the direction of motion is not given. This is because the direction a ferris wheel turns depends on which side of the wheel we are viewing it from. So you will need to choose which direction you want to model the wheel's motion in: for these problems, you will get the same results regardless of which direction you choose (unlike other problems where the directions are specified).
In problems where two people are moving in opposite directions on a circle, the time until their first pass can be found by determining the sum of the angles that they each run through to reach that first pass, and then divide that angle by the sum of their angular speeds. Note that the additional time for the second pass (i.e., the amount of time from the first pass to the second pass) will be 2 pi divided by the sum of their angular speeds. This additional time will be the same for every pass from then on.

May 13, 2017

Here are particular problems from the exam archive that you should use for practice. Other problems on the exams mentioned can be skipped.

All exams referred to are second midterms.

Winter 2017: problems 2, 3, 4
Autumn 2014: problems 1, 3, 4
Autumn 2013: problems 1, 2, 4
Spring 2013: problems 1, 3, 4
Winter 2013: problems 2, 3, 4
Autumn 2012: problems 2, 3, 4
Winter 2012: problems 1, 3, 4
Autumn 2011: problems 2, 3, 4
Spring 2011: all problems
Winter 2011: problems 2, 3, 4
Winter 2010: problems 2, 3, 4

May 12, 2017

Midterm 2 is coming up next Thursday, May 18. It will cover chapters 8 through 16. Trigonometry problems will not appear on the exam.

The exam will have 4 questions.
You will have 50 minutes to complete it.
The only electronic device you can use during the exam is a TI30XIIS calculator. All other electronic devices must be turned off and put away for the duration of the exam.
You may bring a single two-sided, hand-written 8.5 by 11 inch sheet of notes. You can write anything you want on it.

Comments on today's lecture:

Trigonomertry: We start with the definitions of sin θ, cos θ and tan θ for an angle θ appearing in a right triangle. Together with algebra (and the fact that our calculator can calculate these values for any given θ) we can solve many problems expressible in terms of unknown triangle side lengths.
We extend these definitions beyond the triangle using the unit circle: sin θ, cos θ and tan θ are meaningful for all θ not just those that might appear in a right triangle. This gives us the power to use sin, cos and tan to solve other kinds of problems.
Circular motion We began our discussion of circular motion today. We want to be able to model motion of an object on a circle, with constant speed and direction (analogous to what we did with uniform circular motion). We will discuss this more after the second midterm exam. This material will not be covered on the exam.

May 10, 2017

Comments on today's lecture:

Angular speed and linear speed Anything that turns, rotates, revolves, etc. has both an angular speed (measured in units like revolutions per minute, degrees per second, etc.) and a linear speed (measured in units like miles per hour, meters per second, etc.). Linear speed is really just plain old speed, but in this context it is helpful to call it linear speed to distinguish it from angular speed.
The key relationship between linear speed, angular speed, and the radius is expressed by the equation v=r ω, where v is the linear speed (v for velociy), r is the radius and ω is the angular speed expressed in radians per unit time (e.g., radians per second or radians per day). We didn't derive this equation in lecture, so let me do that here. If an object moves with angular speed ω, then it takes 2 pi/ω units of time to make one revolution or rotation. In traveling through one rotation, a point on the edge of the rotating object moves through a distance equal to the circumference of the circle with radius r: that is, through a distance of 2 pi r. Hence, the linear speed of the object is equal to v = (2 pi r)/(2 pi /ω) = r ω.
Two object that are attached to the same axle and rotate together, so that a rotation of one results in an equal rotation of the other (such as the rear sprocket and the tire or a wheel), have the same angular speed.
A wheel rolling on the ground has a linear speed equal to the speed at which it rolls. So, for instance, a wheel on a car moving 100 kph has a linear speed of 100 kph.
Two sprockets connected by a chain, or two pulleys connected by a belt, so that the rotation of one necessitates the rotation of the other, have the same linear speed. We can argue for this by noting that, if one sprocket moves at a constant linear speed, then a point on the chain must also move at that linear speed, and so the other sprocket must also.

May 8, 2017

Comments on today's lecture:

Circular measure Threes units of circular measure that we will be working with are the degree, the radian, and the revolution. One revolution equals 360 degrees equals 2 pi radians.
A circular section with radius r and angle theta has area equal to (1/2)r² theta and arc length (i.e., the length of the curved part) r theta, when theta is in radians. The simplicity of these expressions compared to the corresponding ones for theta in degrees shows some of the benefits of working with radians versus degrees.

Comments on Friday's lecture

Linear to linear rational functions A linear to linear rational function is one of the form f(x) = (ax+b)/(cx+d). By dividing the numerator and denominator by c, we can always write such a function in the form f(x)=(Ax+B)/(x+D), and we will use this form in applications (e.g., when we are trying to determine the linear to linear function that satisfies certain requirements). Note that when we write (ax+b)/(cx+d), we are assuming that c is not zero, since, if it were, the function would simply be a linear function.
Graphs: All graphs of linear to linear functions are shifted/scaled/flipped versions of the graph of y=1/x, so be sure to know that curve well. Its main features are a vertical asymptote and a horizontal asymptote, features it shares with all linear to linear rational functions.
The function f(x)=(Ax+B)/(x+C) has y=A as its horizontal asymptote and x=-C as its vertical asymptote.
Since the function f(x)=(Ax+B)/(x+C) is determined by three parameters (A, B, and C), three pieces of data are needed to nail down such a function. This data can come to us in one of three ways: (1) three points, (2) two points and an asymptote, and (3) one point and two asymptote. Be sure you are prepared to determine the linear to linear rational function specified in each of these three ways.
In applications, the horizontal asymptote is often described by saying that a quantity is always increasing (or decreasing) but never exceeds (or drops below) a certain value. Alternatively, it might be described by saying that as time goes on, the quantity gets closer and closer to a certain value. The value then represents the horizontal asymptote of the sought linear to linear rational function.

May 3, 2017

Comments on today's lecture

Given a function f(x) whose graph we know, we can determine (e.g., sketch) the graph of g(x)=Af(Bx+C)+D for any constants A, B, C, and D. This greatly expands the set of function's whose graphs we can know.
The main idea is that the graph of g can be seen as created from the graph of f via a series of shifts, dilations, and flips.
The graph of g(x)=f(x+a) is the graph of f shifted a units to the left.
The graph of g(x)=f(bx) is the graph of f stretched away from, or compressed toward the y-axis (depending on whether b is less than, or greater than, 1 in absolute value). If b is negative, the graph also flips across the y-axis.
The graph of g(x)=cf(x) is the graph of f stretched away from, or compressed toward the x-axis (depending on whether c is greater than, or less than, 1). If c is negative, the graph also flips across the x-axis.
The graph of g(x)=f(x)+d is the graph of f shift d units upward.
To graph g(x)=Af(Bx+C)+D, first factor the B to get g(x)=A(f(B(x+C'))+D, say. Then graph, in sequence, f(Bx), f(B(x+C')), Af(B(x+C')), and finally Af(B(x+C'))+D. Each graph is a modification (either a shift or a dilation, and possible a flip) of the previous one.

May 2, 2017

Here is a mechanical review sheet for the second midterm.

Comments on Monday's lecture:

Exponential modeling One of the primary challenges in problems of exponential modeling is the need to recognize that you are being asked to use exponential functions. There are several ways that an exponential function may be indicated. We might be told that a quantity has a constant doubling time or we might be told that a quantity increases by a fixed percentage every year (or other time period). We might of course simply be told that a quantity is growing exponentially.
Exponential functions are encountered in two common forms: A₀ b^t and A₀ e^rt. Given one form, you should be able to convert to the other.
Given information about a quantity growing exponentially, we need to be able to determine the function that expresses the value of the quantity at any time. Since an exponential function has two constants, two points (the value of the function at two time) is enough information for us to work out the function.
Generally, when working with years, we will want to set a time reference point. That is, we will want to specify that t=0 represents a certain year. If we do not do this, and try to use t as the year, then we run into the issue that our A₀ values may be very small; sometimes, they will be so small that our calculators cannot represent them. For instance, suppose a population is growing at 2% per year, and it was 1 million in the year 2000. Then, using t as the year, the population is equal to
(6.3045846 x 10^-12)(1.02)^t. More simply, we can express it as (10⁶)(1.02^t) with t in years after 2000.
The doubling time gives us all the information we need to determine the base value ("b"). If it takes D years to double, then A₀b^D = 2 A₀, and from this we can solve for b.

April 28, 2017

Comments on today's lecture:

The exponential function. We often refer to the function e^x as the exponential function. It is easily the most famous and important function in all of mathematics. Its inverse is the natural logarithm, ln x. Both functions have played a major role in the history of mathematics and science and continue to be incredibly useful and important.
The natural logarithm has several nice properties that make it a powerful tool. For us, the most important one is that, applied to an exponential expression, it yields a linear expression, and so it converts what we might call exponential equations into linear equations. Since we can solve linear equations, this is good.
Other logarithms exist. For any b>0, the exponential function b^x has an inverse; we call it the base b logarithm, written log_b. We rarely need these functions however, since they are merely constants times the natural logarithm: log_b x= (ln x)/(ln b).

April 26, 2017

Comments on today's lecture:

Exponential functions Exponential functions are functions of the form f(x)=A₀ b^x where A₀ is non-zero, b is non-zero, and b is not equal to one. The notation A₀ arises from the fact that, with f(x)=A₀ b^x, we have f(0)=A₀.
The graphs of exponential functions all look essentially the same, in the same way that all graphs of linear functions are lines, and all graphs of quadratic functions are parabolas. The most interesting feature of the graphs of exponential functions is the asymptote, a feature not found in linear or quadratic functions.
The product and quotient of any two exponential functions are exponential functions. Compare this to linear and quadratic functions for which the sum of two functions is linear or quadratic, respectively. As well, certain compositions of exponential functions and linear functions will be an exponential function. In particular, of f(x) is linear and g(x) is exponential, then g(f(x)) is exponential. Be sure to practice the necessary algebra to simplify expressions created by combining exponential and other functions.

April 26, 2017

Comments on Monday's lecture:

Inverse functions Two functions f and g are inverses if f(g(x))=g(f(x)) for all x in the domain of f and g. The term inverse comes from the fact that, if f and g are inverses, and we "plug" a number A into f to get f(A), we can take that result and plug it into g to get A back: A = g(f(A)). In other words, g undoes the action of f, and vice versa.
Not all functions have inverses For a function f to have an inverse, it must be true that there are no values x₁ and x₂, with x₁ not equal to x₂, for which f(x₁)=f(x₂). For example, if f(x))=x², then we find f(1)=f(-1). From this we can conclude that f has no inverse. Why? Well, if we know that 1 came out of f, we cannot know with certainty what went into f, and being able to say with certainty what went into f is what is needed in order for f to have an inverse. Functions for which f(x₁)=f(x₂) always implies x₁=x₂ are known as one-to-one functions. All functions with inverses are one-to-one functions, and all one-to-one functions have inverses.
Horizontal line test The requirement described above can be put in graphical terms: a function has an inverse only when horizontal lines intersect its graph at most once. In this way, if we know enough about the graph of a function, we may be able to conclude whether or not it has an inverse.
Finding an inverse function Given a one-to-one function f, we can find the inverse of f by solving the equation f(x)=y for x. If we succeed, we will have the inverse expressed via x=f^-1(y). That is, the expression on the right will be the inverse of f expressed using the variable y.
A nice fact connects the graph of f and its inverse: they will be "mirror images" of each other across the line y=x. This is becuase, if (a,b) is in the graph of f, then (b,a) is on the graph of f^-1.
Restricting domains For some functions that are not one-to-one, it is possible to restrict the domain of the function to get a function that is one-to-one. For instance, the function f(x)=x² is not one-to-one, but the function f(x)=x² for x≥0 is one-to-one. The former has no inverse, but the square root of x is the inverse of the latter. In the homework, the main application of this idea is to quadratic functions: by cutting the graph in half with the vertical line through the vertex, and taking one half or the other as the graph of the function of interest, we get a one-to-one function.

April 24, 2017

Statistics from the first midterm: n=145; min=4; 1st quartile=20; median=27; 3rd quartile = 31; max=40 (5 students)

Here is a histogram of the scores:

Here is a table of score to 4.0-scale conversions. This is only to give you a rough idea of how you did on the exam: I do not use these converted values for any purpose.

≤15 0.0

16 0.6

17 0.8

18 1.0

19 1.2

20 1.4

21 1.6

22 1.8

23 2.0

24 2.2

25 2.4

26 2.6

27 2.7

28 2.8

29 2.9

30 3.0

31 3.1

32 3.2

33 3.3

34 3.4

35 3.5

36 3.6

37 3.7

38 3.8

≥39 4.0

April 23, 2017

Answers to the first midterm exam are now on the 120 Materials Website test archive.

April 22, 2017

Residues from Friday's lecture are now on the discussion board.

Comments on Friday's lecture:

Composition We can combine functions into new functions using the four operations of arithmetic, just as we can with numbers. Composition is an additional way that we can combine functions into a new function that has no parallel with numbers. For functions f(x) and g(x), the function f(g(x)) is the composition of f with g. We can also compose g with f to get g(f(x)). Order matters: generally, f(g(x)) is not the same function as g(f(x)), though they can be the same. Be sure to practice the mechanics of composing functions: given any f(x) and g(x) that you've seen in the course, you should be able to give an expression for f(g(x)) as simply as possible.

One question: for what functions f(x) is f(f(x))=f(x)?
Decomposition A useful mental framework for thinking about functions arises from the fact that we can often usefully write a function as a composition of simpler functions. For example, f(x)=(2x+3)^2 can be expressed as the composition of g(x)=x^2 and h(x)=2x+3: f(x) = g(h(x)).
Fixed points For a function f(x), its fixed points are all values of k for which f(k)=k. Functions may have any number (including zero) of fixed points, and could have infinitely many. Finding fixed points is straight0-forward: set f(k)=k and solve for k: any solutions you get are the fixed points of f(x). Some good questions to figure out: What are some functions with no fixed points? What are some functions with one fixed point, or two fixed points? Can we find a function which has only 2 and 5 as fixed points?

Fixed points are related to composition in that, if k is a fixed point of f(x), then k is a fixed point of f(x) composed with itself any number of times (i.e., f(f(x)),f(f(f(x))), etc.). These compositions can have other fixed points, too, but k will always be one of its fixed points.

April 19, 2017

Residues from today's lecture are now on the discsussion board.

Good luck on tomorrow's exam!

April 17, 2017

This is a reminder that the midterm exam is this Thursday in your quiz section, at the usual time and location.

The exam will have 4 questions.
You will have 50 minutes to complete it.
The only electronic device you can use during the exam is a TI30XIIS calculator. All other electronic devices must be turned off and put away for the duration of the exam.
You may bring a single two-sided, hand-written 8.5 by 11 inch sheet of notes. You can write anything you want on it.

April 17, 2017

Comments about today's lecture:

We looked at more quadratic optimization examples. There are three types of quadratic optimization problems you want to be prepared for for this week's midterm:
- Geometric (e.g., enclosing the rectangle of maximal area with a given amount of fencing)
- Ticket/fruit problems (that is, problems where a quantity Q(x) is a linear function of x, and we are interested in xQ(x): since Q(x) is linear, xQ(x) is quadratic so we can optimize it)
- Uniform linear motion closest approach (if two objects exhibit uniform linear motion, then the distance between them will be the square root of a quadratic function of time; to minimize the distance, we can minimize this quadratic function)
I posted a mechanical review sheet (link below) that you might use in preparation for the midterm. You should be prepared to use all the skills listed, plus other skills as needed (e.g., reading carefully, drawing a figure, imposing coordinate systems, etc.)

April 16, 2017

Here is a mechanical review sheet for midterm 1.

April 14, 2017

Lecture residues have been posted on the discussion board. Comments on today's lecture:

Quadratic optimization In general, if we want to maximize or minimize a quantity expressible as a quadratic function of one variable, we can do by using our knowledge of the graphs of quadratic functions. The vertex plays a key role here. In this course, there are three categories of problems involving quadratic optimization:
Geometric optimization These are problems where we have a limited amount of material to construct a plane figure, and we wish to maximize (or, less often, minimize) the area of the figure. The usual method here is to express the area in terms of two dimensions of the figure (like length and width), and then use the fact that material is limited to write a constraint involving the two variables; then, using the constraint equation, we can solve for one of the variables in terms of the other, and substitute this into the objective function. The result will be a quadratic function of one variable, and so we can use our knowledge of the graph of such functions to answer the question.
Linear relationships times the variable (Not a very catchy name) This category of problems involves a variable x, a decreasing linear function T(x), and their product xT(x). Since T(x) is linear, xT(x) will be quadratic, and we can use our quadratic function graph knowledge to analyze and solve the problem. Examples of this include: (a) x is ticket price, T(x) is number of tickets sold at price x, and so xT(x) is the revenue from sold tickets, and (b) x is the number of trees in an orchard, T(x) is the number of apples produced per tree as a function of the number of trees, and xT(x) is the total number of apples produces.
Closest approach of two moving objects If two objects move with uniform linear motion, then the distance between them can be expressed as the square root of a quadratic function of time. To minimize this distance (i.e., to find when the objects are closest together), we minimize this quadratic: the time what the quadratic is minimized is the time when the distance is minimized. One nice feature here is that, regardless of the equations of motion, the quadratic will always be an "opening upward" one, so the vertex will always yield the minimum distance.

April 12, 2017

Comments on today's lecture on quadratic functions:

Graphs of quadratic functions The graph of a quadratic function is a parabola, opening upward when a>0 and downward when a<0, with line of symmetry x=h, and vertex (h,k), where the function is given by f(x)=ax²+bx+c=a(x-h)²+k. So, to graph a quadratic function, we must find the vertex. Plot the vertex, note whether a is positive or negative, and you can make a basic sketch of the graph of the function. The value of a determines how wide or narrow the parabola is. We can make our sketch more precise by adding just one more point ( really two, but we get the second one for free using the symmetry of the parabola). Any point other than the vertex can be used here to clarify the shape of the graph.
Determining a quadratic function given by three points Three points are needed to determine a quadratic function (that is, given two points, we can find infinitely many quadratic functions with graphs passing through those two points, but if three points are specified, then only one quadratic function is possible). If we know that (x₁,y₁),(x₂,y₂), and (x₃,y₃) are three points on the graph of a quadratic function f(x), then we have f(x₁)=y₁, f(x₂)=y₂ and f(x₃)=y₃. With f(x)=ax²+bx+c, we can use these three equations to get three equations in a, b, and c and then solve for c.

When we get these three equations, a nice thing to notice is that they all end in "+c". So, a good approach is to subtract the equations in pairs (the first from the second, and the second from the third, say) to eliminate c and get two equations in a and b, and then solve for a and b, and then c. In this way, we can find f(x).
Maximum and minimum values of a q.f. on an interval Because we can so completely understand the graph of a quadratic function, we can determine the maximum and minimum values of a quadratic function on an interval. A quadratic function f(x), considered on the interval r <e; x <e; s, will attain its maximum and minimum values at the vertex, or at the endpoints. So, to find the maximum and minimum values, we can find f(r), f(s), and k (the y-value of the vertex). The largest of these three values is the maximum, and the smallest of these values is the minimum.

April 10, 2017

Some comments on today's lecture:

Piece-wise uniform linear motion The motion in the first example in today's lecture might be called piece-wise uniform linear motion. That is, uniform linear motion is happening at any instant, but there are occasional changes of direction and/or speed. As in today's example, the key thing is to get expressions for the location of the moving object at a time t since the start. You will need a pair of expressions (x and y) for each portion of the path on which speed and direction are constant. In today's example, there were three such portions, and so we needed three pairs of expressions. Once we have all of these expressions, we will have a complete handle on the motion, and so can answer any question about it.
Multipart function from a graph involving circular bits We already know how to find equations of lines, so if we are presented with a graph of a multipart function made up of line segments, we have the tools to determine the function. We can also deal with graphs that involve pieces of circles, by solving for the circle equations and choosing the ± appropriately. We can use the fact that we want the + when our circular piece lies above the circle's center, and we want the - when our circular piece lies below the circle's center.
Solving equations involving multipart functions When we want to solve an equation of form f(x)=g(x), where f(x) is a multipart function, we need to create a set of equations, one for each part of f and solve each one. We will need to check whether or not our solutions satisfy the corresponding condition in the multipart rule. Alternatively, we can directly plug our "candidate" solutions into our original equation and see if the equation is satisfied.

April 7, 2017

Lecture residues are posted on the discussion board.

Some comments on today's lecture:

When working with functions involving absolute value, writing the multipart rule for the function can be very helpful. To do this, we want to utilize the multipart rule for |x|. The general idea is that |f(x)|=f(x) wherever f(x)> 0 and |f(x)|=-f(x) wherever f(x)<0.
Pizza problems Although these problems can be approached in a variety of ways, the method illustrated in class will treat all of them well. The steps can be boiled down to:
1. Draw a picture of the 'pizza' on a coordinate system, with the origin at the lower left corner and the x-axis along the lower edge.
2. Find the coordinates of all vertices (corners) of the pizza.
3. Find the equations of all lines making up the upper edge of the pizza.
4. Use the fact that a line equation y=mx+b for a portion of the upper edge tells you the length of the cut at x, so use this length in your calculation of the area of that portion of the pizza. You want a function of x that expresses the area to the left of the cut.
5. Do this for each portion of the pizza.
6. Combine all expressions into a single multipart rule.
I strongly encourage the use of the trapezoid area formula. Work to see trapezoids in your work: this will save you time and effort over other methods.

April 5, 2017

Some comment on today's lecture:

Functions Functions are one of most important concepts in all of mathematics. We'll be talking about functions for the rest of the quarter, and you'll continue learning about functions in your calculus courses: there is no end to the study of functions!
Notation One thing that trips up many people is the notation of functions. Consider the function with the rule f(x)=2x+5. With this, we can say, for example
- f(3)=2(3)+5 = 11
- f(u) = 2u+5
- f(u+1) = 2(u+1)+5 = 2u+7
- f(x+4) = 2(x+4)+5 = 2x+13
Note that in each case, the x's that appear on the right side of rule get replaced by whatever expression we have replaced x by on the right. You might think of the rule as saying f(_) = 2(_)+5 where the blank must be filled in by the same expression.

Where we might need to be particularly careful is the situations where the rule has more than one instance of the variable on the right. For example, suppose g(x)=x^2-x. Then we can say, for example,
- g(4) = 4^2-4 = 12
- g(u+1) = (u+1)^2-(u+1)
- g(x-3) = (x-3)^2-(x-3)
Be sure to practice this sort of notational manipulation carefully so that it becomes second nature!
Domain, range and graphs Three things associated with every function are its domain, its range and its graph. Often the domain is relatively easily determined, but the range is often challenging: in many cases, we would need calculus to determine the range of a functions, and even with calculus there are many functions whose ranges are not determinable. So, we'll be taking things very carefully, looking only at certain classes of functions for which we'll be able to determine the ranges.

Likewise, graphing is hard. By restricting our consideration to just certain classes of functions, we'll be able to build up our knowledge of graphs of functions. You'll get many more tools for studying graphs in calculus.

April 3, 2017

In today's lecture, we hit on the following points:

Uniform linear motion When things move in the xy-plane along a line at constant speed, then we can model their movement using two equations that relate x and y to time. We get x=a+bt, y=c+dt, where t is the time since the thing started moving, and a, b, c, and d are constants.

Notice that if we let t=0, then we have x=a, y=c, so the point (a,c) is the "starting point" of the moving thing.

The b and d values determine the speed and the direction of motion. If b is positive, the thing is moving to the right, and if b is negative, the thing is moving to the left. If d is positive, the thing is moving upward, and if d is negative, the thing is moving downward. We can think of b as the rate at which the x-coordinate changes (aka the horizontal speed) and d as the rate at which the y-coordinate changes (aka the vertical speed).
Flavors of information about uniform linear motion To determine the equations of motion (i.e., x=a+bt, y=c+dt), we have four things that we need to figure out (i.e., a, b, c, d). So, we need four pieces of information in the description of the motion to be able to do this. The best situation is to know two locations corresponding to two times: this gives us two x-coordinates and two y-coordinates, so four pieces of information. With this information, and a small amount of algebra, we can find a, b, c, and d. If our information about the motion comes in a different form (e.g., we might know the line the motion occurs on, the start location, the speed and the directions), then we will want to get into that simplest situation of two times and two corresponding points, so that we can solve for a, b, c, d. So, we will need to find two points and two corresponding times from the information given.
Parametric equations encode everything about the motion Looking at things in reverse, we saw that if we have the equations of motion x=a+bt and y=c+dt, then we can determine the line along which the motion happens, the speed, the direction, and the starting location. This is all encoded in the parametric equations, and is part of what makes this method so powerful.

March 31, 2017

In today's lecture, we hit on the following points:

Imposing a coordinate system In today's example, we had a few points that could have been used as the origin of a coordinate system. However, due to the way the points' locations were described, and the fact that one point would be the center of a circle, it became clear that choosing the fountain as the origin would be a good choice. There is no wrong choice; some choices might give us a system that is a little easier to work with than the system we would get with another choice.
Finding the equation of a line Given two points, we can find the equation of the line passing through them. We will do this a lot, and it will come up quite a bit in Calculus, so it is something you want to become very smooth with. I strongly recommend the point-slope form: if the slope is m, and the point passes through (x₀,y₀), then the line has equation
y=m(x-x₀)+y₀. This is very efficient: we don't need to solve for anything or do any algebra to get this line form. If we want, we can simply multiply the m through to put it in the form y=mx+b. Using this method introduces the fewest number of places where you might make an error; that is why I recommend it.
Intersection of a line and a circle Given a line y=mx+b and a circle x²+y²=r², we find the intersection by solving the equation x^2<+(mx+b)²=r². We can note early that this is a quadratic equation, and so we can know that we will be able to solve the equation. This is one place where we will need to square a linear expression (to treat (mx+b)²) so be sure to practice this enough to get smooth. In general, you should use the fact that (A+B)²=A²+2AB+B² often, to save time, and, again, use fewer steps and hence have fewer places for errors to happen.

Note that when intersecting a line and a circle, we could end up with zero, one or two points of intersections; the quadratic formula will tell us how many there are.
The quadratic formula will give us the x-coordinates of the points of intersection. You then need to plug those x-coordinates into the line equation to get the y-coordinates. Note that you could utilize the circle equation to get the y-coordinates, but this is more work, since you'll need to square root something, and you'd have to decide whether to pick the positive or negative root, and it's just not worth it! Just plug into the line equation to quickly get the y-coordinates.
Shortest distance between a line and a point Given a line and point not on that line, we want to be able to find the distance between the line and the point. To do this, we want to find the point on the line that is closest to the given point. Say our given line is y=mx+b and the point not on the line is P. Then what we need to do is find the line through P that is perpendicular to y=mx+b. This line will have slope -1/m, and since it passes through P, we can find the equation of the line. The intersection of this line, and the original line, will be the point on the original line that is closest to P.

If a problem asks us how close something moving along the line comes to the point P, we would then want to find the distance from the intersection point to P (using the distance formula).

March 29, 2017

In today's lecture, we hit on the following points:

Drawing a picture and imposing a coordinate system These two steps often happen at the same time: we might say that we draw a picture of the scenario using the coordinate system as a reference. These two steps are critical to many problems in this course.
Imposing a coordinate system in time We often want to use a variable t to represent time, but we need to be sure what we are doing with this. In one example today, we explicitly set t=0 to represent noon. In other problems, we might say "t=0 is the time when Maria starts moving", or some other phrase that nails down what the variable t actually represents. If there is more than one thing/person moving, we want to be careful to use t the same way for both, so we should make one definitive statement of what t=0 means and use it throughout the problem.
Motion in the plane In particular, we talked about constant-speed horizontal or vertical motion. We saw that the location of something that is moving in this way can be expressed in the form (a±vt,c) or (c,a±vt) (the former if moving horizontally, and the latter if moving vertically; the ± is chosen based on whether the motion is to the left/upward or to the right/downward).

We will talk about constant speed motion in any direction soon.
Distance formula We will use the distance formula a lot in this course, so be sure to have it nice and clear in your mind.
Quadratic formula We will use the quadratic formula a lot in this course; be sure you know it so you can use it correctly and without hesitation. One thing to note is that it can be easier to solve a quadratic equation without the quadratic formula when possible. In particular, if b or c is zero, then there are easier things to do.

For example, consider the equation ax²+bx=0 (so this is a case where c=0). By factoring an x, we have x(ax+b)=0, so either x=0, or ax+b=0, i.e., x=-b/a. No quadratic formula needed!

March 27, 2017

I asked everyone to fill out and return a survey to give me information about everyone.

Here are my answers to the survey questions.

Hometown: I lived in Billerica, Massachusetts, until I was 10, and then my family moved to Oxnard, California, where my parents still live. I generally think of Oxnard as home, though I've now lived in Seattle quite a bit longer than I ever lived in Oxnard.
Hobbies or interests: When I'm healthy and the weather's not too bad, I ride my bicycle a lot. I draw, usually with charcoal and/or pencil (I am often at Gage Academy's figure drawing open studios). I like creating algorithmic visual and sound art. I am a fan of movies from the 1920s to 1940s especially.
One of my favorite books, movies or bands: I like Richard Brautigan's Trout Fishing in America, Knut Hamsun's Hunger and Fyodor Dostoevsky's The Idiot. I like It's a Wonderful Life, The Seventh Seal, and Night of the Hunter. I like Einsturzende Neubauten, The Mountain Goats and Neutral Milk Hotel.
What's an interesting, exciting or memorable thing you've done? I've ridden up Alpe d'Huez.

March 27, 2017

I'll be scanning and posting the paper that I write on during lectures (I call these my "lecture residues"). You can find them on the discussion board here.

A good way to view your learning in this course is as the development of a toolbox. We will be adding tools to the toolbox, sharpening tools, and practicing with those tools.

In today's lecture, here are some tools we used:

Drawing a picture
Introducing variables for unknowns
Translating sentences into equations
Recognizing a two-equations-in-two-unknowns situation

good

Solving a system of two linear equations in two unknowns
Checking our work by substituting our solutions into our earlier equation

We started with the equations (l+1)(w+1)=20+lw and (l+2)(w+3)=50+lw and found w=13 and l=6.

To check these values, we want to evaluate each side of the two equations and see if they are equal.

With w=13 and l=6, we find (l+1)(w+1) = (7)(14) =98, while 20+lw = 20+(6)(13) = 20+78=98, so the first equation is satisfied.

Likewise, with w=13 and l=6, we find (l+2)(w+3) = (8)(16) = 128, while 50+lw=50+(6)(13)=50+78=128. So the left and right sides of the equation equal 128, and so the second equation is satisfied, too.

Thus, we can conclude that our work in solving for l and w was correct.

Notice that checking calculations is a good idea for at least two reasons. If we find that our calculations were wrong, then we can avoid using up a WebAssign attempt (you only have five for each problem). Also, on the exam, there is "red x, green check" feedback, so it will be helpful to practice checking your work so that you can do it during exams and perhaps catch and correct your own errors.

March 25, 2017

Welcome to Math 120 A Spring quarter 2017.

Announcements and other useful things will be posted here during the quarter.

Textbook: The textbook for this course is Precalculus, by Collingwood, Prince and Conroy. The book can be purchased at the UW Bookstore.

You do not have to purchase the textbook. It is available electronically: here is a direct link to the pdf.

Reading schedule: I have started a reading schedule (see the link at right) so you can stay on top of course topics, access all additional course materials, and get the most from lectures.

Discussion Board: The course has a discussion board (link at right). This is a great way to ask questions of me in a way that will benefit all students in the course. You can ask about homework questions, studying methods, etc. You can also use it to coordinate study sessions with other students.

Homework: We will be using WebAssign for homework.

WebAssign: You can log in to WebAssign here. This will require your UW Net ID. Your UW Net ID is the part of your university email address before the @ symbol. The password to log in is your UW Net ID password.

You must be enrolled in the course in order to get access to the homework on WebAssign.

You will need to purchase an access code before the grace period ends. You can purchase an access code on the WebAssign website after logging in.

The first homework assignment will be due on the night of Thursday, January 12.

If you are not enrolled in the course, but are trying to add, you can get started on the homework without WebAssign by working the following problems in the textbook (which is freely available here).

Chapter 1: problems 1-10, 14,15
Chapter 2: 2-7, 10, 12, 13

These problems will have different numbers than the ones you will have on WebAssign, but if you write out solutions for these, it won't be too much trouble to rework them with the WebAssign values.

These problems will cover you through the first homework assignment.

I will periodically be expounding here on aspects of the course, particularly study methods and problem-solving tools.

Reading the problem This is an often overlooked key step in problem-solving. Be sure to always read the problem carefully, at least twice through before you begin solving the problem. A great way to fail to solve a problem is to attempt to solve a problem that wasn't asked, so make sure you are solving the problem you are given.

I think this is especially true during exams, where you cannot ask for help, or go away and come back to it the next day. So dedicate the first minute or two of work on each exam problem to reading slowly and carefully to be sure you are solving the right problem.

Introducing time variables We've seen in lecture that if an object it moving horizontally at a constant speed in the plane, then its location can be expressed by (A±vt,B), where (A,B) is the "starting location", v is the speed of the object, and t is the time since the object was at the starting location. That is, we are using t=0 to represent that starting time. The plus-or-minus depends on whether or not the object is moving to the right (minus) or left (plus).

A virtually identical method applies to objects moving vertically.

A common issue when using this method occurs when you have more than one object that don't all start moving at the same time. In such a case, you will need to adjust the expression above, keeping in mind that you want to multiply the speed v by the amount of time that the object has been moving since it was at its starting location. In general, this requires replacing t by t+a or t-a for some value of a depending on the start times of your objects.

Rounding and WebAssign In many problems in WebAssign, there is an instruction to round to a certain number of digits. PLEASE IGNORE THIS INSTRUCTION. Instead, keep all digits given by your calculator and enter all of them into WebAssign. I so often see students enter values like 46.5, get a red X, then enter 46.6, thinking that they have rounded wrong, and getting another red X, because their calculation was not correct. A better approach is to enter the full value you get from your calculator (46.51023923, say). In this example, this would still be marked wrong, but you wouldn't waste a second try messing with rounding. I promise that you will never be marked wrong for putting in "too many" digits.

WebAssign attempts For most problems, you have 5 attempts to enter the correct answer (the exceptions are mutliple choice and true-false questions). You should be very stingy about using these attempts. Do everything you can to check your work and your answer before using even the first attempt! Keep in mind that during exams you only get one attempt, so you want to be in the habit of checking your work yourself, and not just relying on WebAssign to tell you whether you have done things correctly.

≤15	0.0
16	0.6
17	0.8
18	1.0
19	1.2
20	1.4
21	1.6
22	1.8
23	2.0
24	2.2
25	2.4
26	2.6
27	2.7
28	2.8
29	2.9
30	3.0
31	3.1
32	3.2
33	3.3
34	3.4
35	3.5
36	3.6
37	3.7
38	3.8
≥39	4.0

Math 120 A - Spring 2017

Instructor:

Dr. Matthew Conroy

TAs:

Exam Dates:

June 8, 2017

May 26, 2017

May 24, 2017

May 22, 2017

May 22, 2017

May 19, 2017

May 13, 2017

May 12, 2017

May 10, 2017

May 8, 2017

May 3, 2017

May 2, 2017

April 28, 2017

April 26, 2017

April 26, 2017

April 24, 2017

April 23, 2017

April 22, 2017

April 19, 2017

April 17, 2017

April 17, 2017

April 16, 2017

April 14, 2017

April 12, 2017

April 10, 2017

April 7, 2017

April 5, 2017

April 3, 2017

March 31, 2017

March 29, 2017

March 27, 2017

March 27, 2017

March 25, 2017

Resources:

Handouts and Supplements

Other UW resources: