Math 307: Gravity and the earth
I may as well restate the problem:
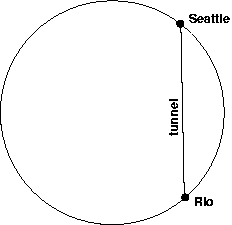
Imagine a train which goes in a
straight line through a tunnel between two points on the
surface of the earth (for example, between Seattle and
Rio de Janeiro). Suppose that there is no friction, and
the train just operates under gravity, so if you start it
at one end of the tunnel, at rest, it will fall into the
tunnel, accelerate until it reaches the midpoint of its
trip, decelerate as it nears the other end, stop at the
other end, and then return. Show that
the time required for a complete round trip is the same
for all such tunnels (it doesn't matter whether it ends at
Rio de Janeiro or Beijing or Baltimore), and estimate its
value.
Facts about gravity:
- The gravitational force between two point masses, of mass
m1 and m2,
respectively, distance R apart, is
-Gm1m2/R2,
where G is the gravitational constant.
- So in general, if you want to compute the gravitation
attraction between two objects, you need to break the objects
into little pieces, compute the forces (as vectors) between
each pair of little pieces, and then add them all up. The
end result of this is an integral. You don't have to do any
such integrals for this problem, because of the following.
- It turns out that if your objects are spheres which are
uniformly dense, the gravitational force is given by exactly
the formula earlier:
-Gm1m2/R2.
(So you could use this to compute the gravitation force
between the earth and the moon, assuming that both are
uniformly dense.)
- Assume that the earth is uniformly dense.
- Now, if a point mass of mass m1 is
beneath the earth's surface, the gravitational force on it is
given by the previous formula, but where
m2 is the mass of the part of the earth
which is closer to the center of the earth than the point mass.
For example, if you're 100 miles from the center of the earth
and you have mass m1, then the gravitation
force on you is
-Gm1m2/1002,
where m2 is the mass of the part of the
earth which is within 100 miles of the earth's center.
For another example, if you're at the center of the earth, the earth
will exert no gravitational forces on you. (Of course, if
you're at the center of the earth, then you're probably
immersed in molten rock or something, so gravity would
probably not be one of your main concerns...)
- Assume that the train in the problem is a point mass.
- You might also need to know the radius of the earth, which
you can look up somewhere. You might also need to know the
gravitational constant G and the mass of the earth,
both of which you can also look up, but if you're clever, you
can just get by with knowing the gravitational force at the
surface of the earth, which is -9.8 meters per second squared.
Hints:
- This problem is dealing with an object (the train) in
motion. So set up a differential equation to describe
that motion.
- (And in this course, we always use the same basic
differential equation when we're dealing with an object in
motion.)
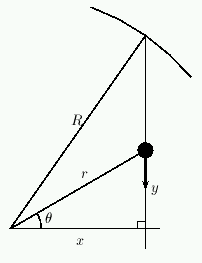
- Here is a possibly useful list of constants and variables,
and also a diagram:
- Let R be the radius of the earth (a constant).
- Let r be the distance from the train to the
center of the earth (a variable).
- The train is traveling along a tunnel; let y
be the distance from the midpoint of the tunnel to the
train (a variable).
- Let x be the distance from the center of the
earth to the midpoint of the tunnel (a constant, for any
particular tunnel).
- Let theta be the angle indicated in the diagram (a
variable).
- In the diagram, the train is the big dot, and it's
traveling in the direction indicated by the arrow.
Questions or comments? E-mail me at palmieri@math.washington.edu.
Back to Math 307 home page.
Go to John Palmieri's home page.
Last modified: Wed Nov 13 14:48:17 PST 2002


