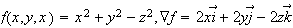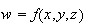
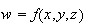
Since we do not have four dimensions to graph such a function, we try to see what it likes by looking at its contours: level surfaces.
The level surfaces for the function
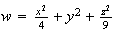corresponding to the values
.
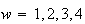Darker colors are for higher function values.
The ellipsoids are graphed with slices removed so that you can see different layers.
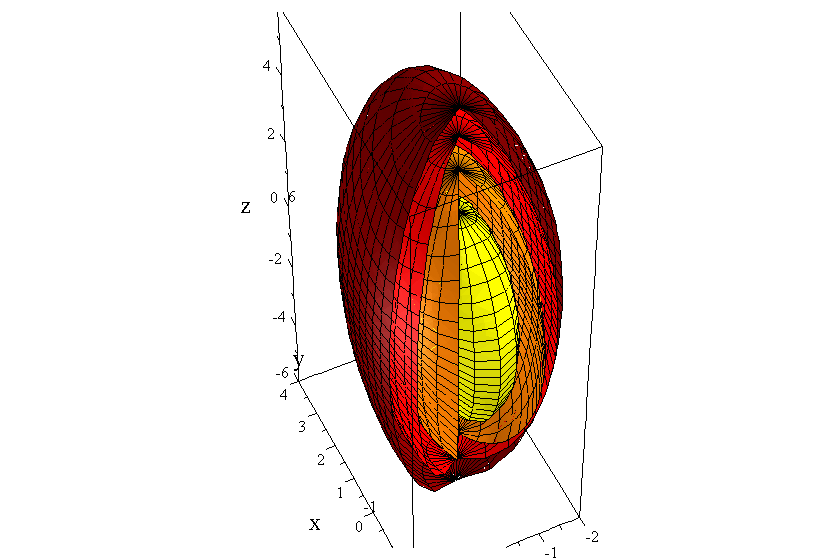
Level surfaces for
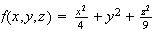
Level surfaces for the function
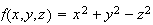corresponding to the values
.
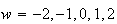The coloring is like a map. Green is for
.
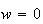Darker blues are more negative. Darker browns are more positive values.
Again, the surfaces are graphed with slices removed so that you can see different layers.
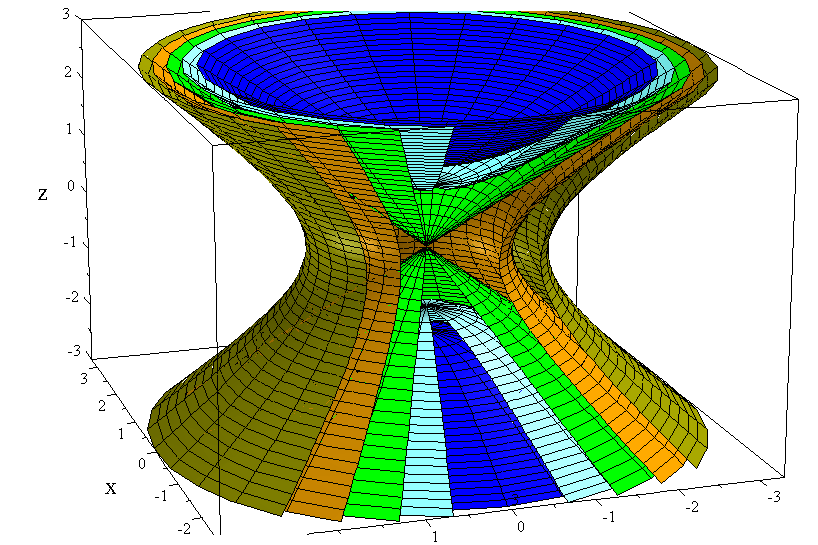
Level surfaces for
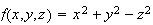
It is not possible to see these on graphs-again 4th dimension problem- but we can say what they are.
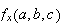is the rate of change when we move from
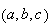in the positive
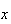-direction
keeping
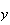and
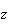constant. To calculate
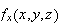we treat
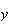and
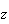like numbers and differentiate with respect to
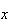with the usual rules of differentiation. Similary, we define
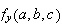and
.
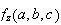For a unit vector
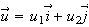
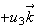we can calculate the directional derivative
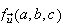by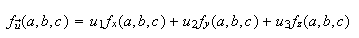
The gradient of
is the
vector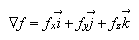
It has the following important properties:
The gradient is a vector in
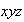-space.
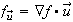
The gradient is always perpendicularto the contours (level surfaces).
The gradient points in the direction of maximum increase for
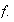
It's length is the maximum possible directional derivative at that point.
As the contours get closer, the size of the gradient increases.
Below
are graphs, contour diagrams and gradients of several functions.
Note that:
The gradient is always perpendicular to the contours (level surfaces).
As the contours get closer, the size of the gradient increases.
For
linear functions, all the contours are parallel and equally spaced.
Also, the gradient vector is the same at every point.
|
|
|
|
The gradient of
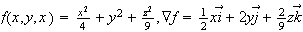
The gradient of
