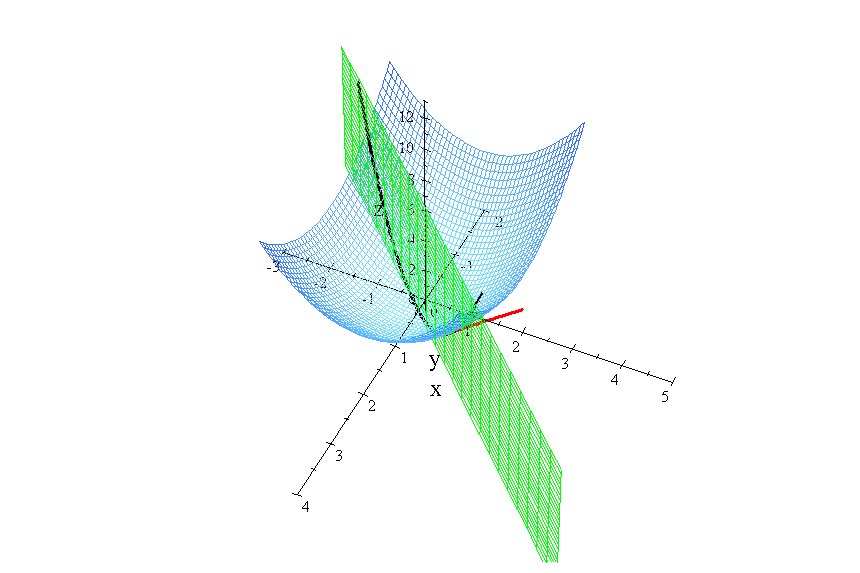
The graph of
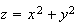 with the tangent at
with the tangent at
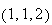 in the direction of
in the direction of
The slope of the red line is the value of the derivative of
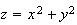 in the direction of the vector
in the direction of the vector
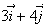 at the point
at the point
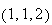 which
is
which
is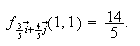
For
a unit vector
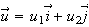 we can calculate
we can calculate
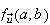 by
by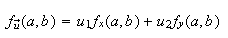
The gradient of
 is the
vector
is the
vector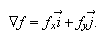 It
has the following important properties:
It
has the following important properties:
The gradient is a vector in
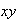 -plane.
-plane.
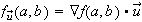
The gradient is always perpendicular to the contours (level curves).
The gradient points in the direction of maximum increase for
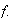
It's length is the maximum possible directional derivative at that point.
As the contours get closer, the size of the gradient increases.
Below
are graphs, contour diagrams and gradients of several functions.
Note that:
The gradient is always perpendicular to the contours (level curves).
As the contours get closer, the size of the gradient increases.
For linear functions, all the contours are parallel and equally spaced. Also, the gradient vector is the same at every point.
|
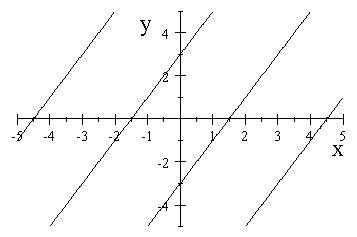
|
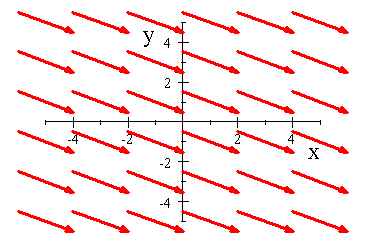
|
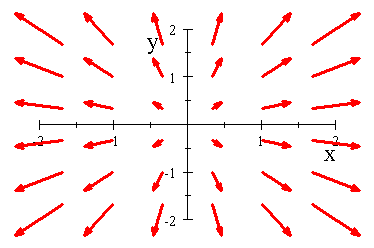
The graph of
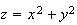 , its contour diagram and several of its gradient vectors. Notice that the
distances between the circles are shrinking and the gradient vectors are
growing in size as you get further away from the origin.
, its contour diagram and several of its gradient vectors. Notice that the
distances between the circles are shrinking and the gradient vectors are
growing in size as you get further away from the origin.
|
|
|
The graph of
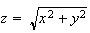 , its contour diagram and several of its gradient vectors.
, its contour diagram and several of its gradient vectors.
|
|
|
The graph of
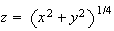 ,its contour diagram and its gradient vectors. Note the distances between the
circles growing are and the gradient vectors are shrinking in size as you get
further away from the origin.
,its contour diagram and its gradient vectors. Note the distances between the
circles growing are and the gradient vectors are shrinking in size as you get
further away from the origin.
|
|
|
The graph of
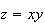 ,its contour diagram and its gradient vectors.
,its contour diagram and its gradient vectors.
|
|
|

The gradient
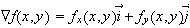 gives a vector for every point
gives a vector for every point
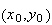 .
.
It is an example of a vector field. (Math 324 or Math 334)
Can you tell what a function looks like by looking at its gradient vectors?
|
|
|
|
|
|
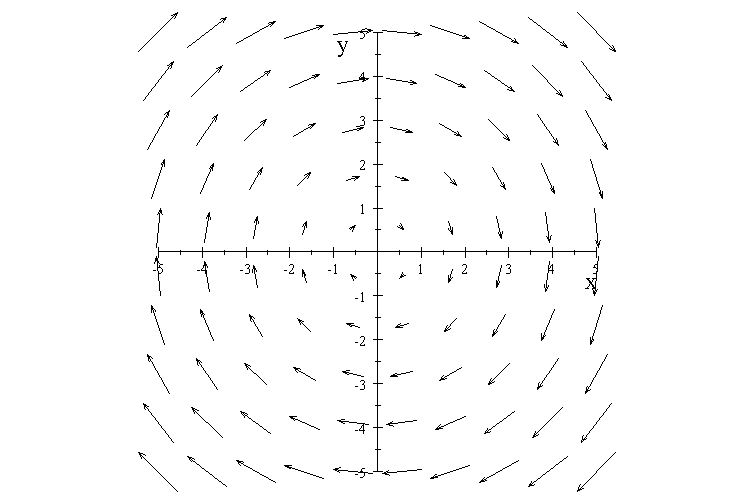
The vector at a given point
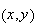 is
is
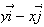
 It is not the gradient of any function.
It is not the gradient of any function.