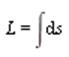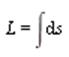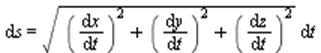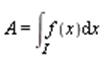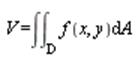Below is a
summary of the calculus on the plane and in space. It is arranged in a table so
you see similarities and differences in different dimensions and objects. It is
not meant to be a complete list of topics or formulas in Math 126. Most of the
first column is from Math 124 and Math 125.
|
xy-PLANE |
xyz-SPACE |
|
|
Describing Curves |
Describing Curves |
Describing Surfaces |
|
y as a
function of x: y=f(x) |
|
z as a
function of x and y : z=f(x,y) |
|
implicitly: F(x,y)=0 |
As an
intersection of two surfaces |
implicitly: F(x,y,z)=0 |
|
Parametrically or
with a vector function: x=f(t),
y=g(t) or r(t)=<f(t), g(t)>
|
Parametrically or
with a vector function x=f(t),
y=g(t), z=h(t) or r(t)=<f(t),
g(t), h(t)> |
Parametrically, using 2 parameters: Coming up in Math
324! |
|
Basic Example of Curves: Lines |
Basic Example of Curves: Lines |
Basic Example of Surfaces: Planes |
|
y=mx+b where m is the slope or ax+by=c. Any linear equation in x and y
describes a line on the plane. |
Intersection of
two planes a1x+b1y+c1z=d1
and a2x+b2y+c2z=d2
|
ax+by+cz=d
with normal vector n=<a, b, c>. Any linear equation in x, y
and z describes a plane in space.. |
|
Parametric/vector form x=x0+at,
y=y0+bt or r(t)=<x0+at,
y0+bt >
with direction vector v=<a, b> |
Parametric/vector
form x=x0+at,
y=y0+bt, z=z0+ct or r(t)=<x0+at,
y0+bt, z0+ct > with direction
vector v=<a, b, c> |
Parametrically, using 2 parameters: Coming up in Math
324! |
|
Differential Calculus |
Differential Calculus |
Differential Calculus |
|
First
derivatives and Tangent lines to curves For a
parametric/vector curve the direction vector for the tangent line at t=t0
is r’(t0). |
First
derivatives and Tangent lines to curves The direction
vector for the tangent line at t=t0 is r’(t0) |
First
derivatives and Tangent planes to surfaces |
|
If y=f(x)
the equation of the tangent line at the point x=x0 is y=f(x0)+ f’(x0)(x-x0) |
|
If z=f(x,y) the equation of the tangent plane at the
point (x,y)=(x0 ,y0
)is z=f(x0,y0)+ fx(x0,y0)(x-x0)+ fy(x0,y0) )(y-y0) |
|
Critical
points and the second derivative test If f has a
local maximum or minimum at x=a and f
is differentiable at a then f’(a)=0. Suppose f’’
is continuous near a and f’(a)=0. If f’’(a)>0,
then f has a local minimum at a. If f’’(a)<0,
then f has a local maximum at a. |
|
Critical
points and second derivatives test If f has a
local maximum or minimum at (x,y)=(a,b) and f is differentiable at (a,b) then fx(a,b)=0 and fy(a,b)=0. Suppose fxx ,fxy,
and fyy are continuous
near (a,b) and fx(a,b)=0 and fy(a,b)=0. Let
If D>0
and fxx(a,b)>0, then f has a local minimum
at (a,b). If D>0
and fxx(a,b)<0, then f has a local maximum
at (a,b). If D<0
, then f has neither a local maximum nor a local minimum at (a,b). |
|
Optimization
on closed and bounded domains If f(x) is
continuous on [a,b],
then it has an absolute maximum and an absolute minimum on [a,b], either at one of the critical points in (a,b) or at one of the endpoints x=a or x=b. (The “boundary”
of [a,b] are its two endpoints.) |
|
Optimization
on closed and bounded domains If f(x,y) is continuous on a closed and bounded domain D, then it has an absolute maximum and
an absolute minimum on D, at one of the critical points inside D or on the boundary of D. |
|
Integral Calculus |
Integral Calculus |
Integral Calculus |
|
The length of a curve r=<f(t),g(t)> is given
by
where
|
The length of a curve r=<f(t),g(t),h(t)>)>
is given by
where
|
|
|
If f(x)>0
on an interval I then the area under the curve y=f(x)
is given by
|
|
If f((x,y)>0 on a domain D then the volume under the surface z=f(x,y) is given by
|