In this paper we prove the Upper Bound Conjecture (UBC) for
some classes of
(simplicial) homology manifolds: we show that the
UBC holds for all odd-dimensional homology manifolds and for all
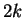
-dimensional homology manifolds
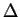
such that
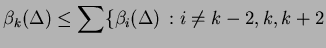
and
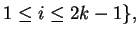
where
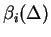
are reduced Betti numbers of
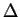
.
(This condition is satisfied by
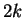
-dimensional homology manifolds with Euler c
haracteristic
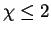
when
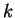
is even or
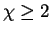
when
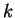
is odd,
and for those having vanishing middle homology.)
We prove an analog of the UBC
for all other even-dimensional homology manifolds.
Kühnel conjectured that for every
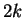 -dimensional combinatorial manifold with
-dimensional combinatorial manifold with 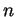 vertices,
vertices,
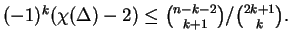 We prove this conjecture for all
We prove this conjecture for all 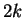 -dimensional homology
manifolds with
-dimensional homology
manifolds with 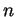 vertices, where
vertices, where
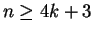 or
or
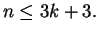 We also obtain upper
bounds on the (weighted) sum of the Betti numbers of
odd-dimensional homology manifolds.
We also obtain upper
bounds on the (weighted) sum of the Betti numbers of
odd-dimensional homology manifolds.
![]() -dimensional combinatorial manifold with
-dimensional combinatorial manifold with ![]() vertices,
vertices,
![]() We prove this conjecture for all
We prove this conjecture for all ![]() -dimensional homology
manifolds with
-dimensional homology
manifolds with ![]() vertices, where
vertices, where
![]() or
or
![]() We also obtain upper
bounds on the (weighted) sum of the Betti numbers of
odd-dimensional homology manifolds.
We also obtain upper
bounds on the (weighted) sum of the Betti numbers of
odd-dimensional homology manifolds.