- Syllabus(dvi)
- Pictures of polyhedra.
- (10/10/95) The definition that I gave of union of two graphs may have confused you. This is the standard terminology, but it would be better if the term was disjoint union, since that is what is meant. If we say G is the union of H and F we mean that H and F have no edges or vertices in common.
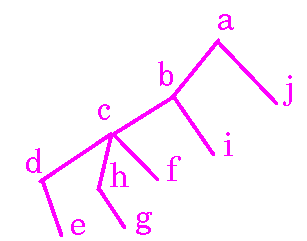
- (10/11/95) After class it was pointed out to me that my use of the term predecessor in the description of the 2-coloring algorithm could be misinterpreted. Maybe it would be better to use the term precursor. In the coloring algorithm, each time a vertex, p, is added to the queue it is because it the neighbor of a uniquely determined vertex, q, that has already been colored. The vertex q will be called the precursor of p. The following picture is a reproduction of the graph discussed in class.

Following another suggestion made in class, we can picture the precursor relationship for this graph by a scheme which is represented by another graph. This graph is a rooted tree. We will discuss trees later in the course. Here is picture of the precursor tree for the coloring algorithm in this case. The precursor of a vertex is the unique vertex immediately above it in this graph. In the coloring scheme a vertex is always colored with the opposite color of its precursor. This coloring can be done at the moment that its precursor is determined. This is an assigment of one of two colors to each vertex of a graph. A 2-coloring results if the graph has no odd circuits.
- (10/12/95) Since I haven't yet covered section 3.4, I will only discuss the homework from section 3.3 on Friday. The home work from section 3.4 will be discussed on Wednesday, October 18. Assigment number 3 will be discussed on Wednesday, October 25.
- (10/16/95) Here is a reference to some interesting projects in discrete modeling: Modules in Applied Mathematics, edited by William F. Lucas, library catalog number QA37.2 .M6 1983 v. 3.
- (10/16/95) I went over the use of the reduction theorem for chromatic polynomials rather quickly. The point I made about computational complexity is the following. The reduction theorem reduces the computation of P(G,x) to the computation of the chromatic polynomials of G-e and G/e. Thus the computation is reduced to the computation of the chromatic polynomials of 2 graphs, each with one fewer edge than G. We can use the reduction theorem on G-e and G/e to reduce the computation to computing the chromatic polynomials of 4 graphs, each with two fewer edges than G. If G has n edges, we can reduce the computation to a combination of chromatic polynomials of 2^n graphs with no edges. The computation grows exponentially with n and is thus impractical.
- (10/17/95) There was a good question asked about the zeros of the chromatic polynomial which I think I densely misinterpreted. If a chromatic polynomial P(x) is 0 for some positive integer value, m, then P(x)=0 for x=0,1,...,m. Also if P(m) is not 0 then P(x) will not be 0 for all integers k>m. I think this is the answer to the question about zeros of P(x).
- (10/24/95) For those of you that are interested in using maple, there are worksheets made up by Greg Arden. They are in the files ~arden/public/{ worksheet1.ms, worksheet2.ms }, which you may copy. Call up maple from a menu or x-window and select file and then open from a maple menu. Then choose one of the worksheet files to open. You will be prompted through the worksheet.
- (10/24/95) Here is a sample of some of the graphics algorithms that are available in maple.
- (10/31/95) Paul Moorehead will give introductory seminars on Maple and Mathematica in Room 3 of Thomson Hall. The schedule is as follows.
- Maple: 3:30-5:00 pm, Wednesday, November 8
- Mathematica: 3:30-5:00 pm, Wednesday, November 15
- (11/2/95) Sample problems for the midterm. The midterm will be on Wednesday, November 8. You will be allowed to bring sheet of notebook sized paper with notes on one side of the sheet.
- (11/3/95) We have applied for and received approval to list Math 381 and 382 as "W" courses. This will apply retroactively. Any student who has taken Math 381 or 382 from me in the last two years will be given "W" credit for the course.
- (11/8/95) Some of you are writing a paper on scheduling projects. Here is a preliminary version of a handout that I have written to summarize the critical path algorithm for project scheduling problems in activity networks.
- (11/13/95) There will be an undergraduate talk by Professor Michael Eastwood on Drawing with Complex Numbers on Wednesday, November 15 at 4:00 pm in Smith 120. Here is the abstract for more details.
- (11/15/95) Here is a handout on scheduling round robin tournaments.
- (11/30/95) This is a reminder that I will be keeping the final version of the paper that you hand in to me. If you want a copy, you should make one before you turn the paper in.
- (12/4/95) On Friday I started the proof of Kruskal's theorem. I mistakenly called it Dijkstra's theorem. Please make that correction in your notes.
- (12/7/95) Here is a set of sample problems for the final exam.
- (12/7/95) There is a colloquium today that might interest you.
Title: The Mathematicians Meet Escher: The Local Theorem for Tilings Speaker: Professor Doris Schattschneider, Moravian College Abstract: The property of a tiling being isohedral is a global one: the symmetry group of the whole tiling must act transitively on the tiles. Yet Escher's isohedral tilings were made according to a local rule: every tile must be surrounded in the same way. The Local Theorem (for tilings in any n-dimensional space) gives a charcterization of isohedral tilings that tells us Escher had the right idea. PLACE: CMU 326 DATE: Thursday, Thursday, Dec. 7, 1995 TIME: 4:00 p.m. -- 5:00 p.m. TEA: 3:30 in the Mathematics Lounge - (12/8/95) Review (dvi) topics.
- (12/9/95) I will have office hours Monday, December 11, and Tuesday, December 12, from 9:30-11:30 am.
- (12/11/95) The final exam is at 2:30 pm on Wednesday, December 13 in the classroom.