Investigating Conics and other Curves Dynamically
James R. King, University of Washington
Interactive software such as The Geometer's Sketchpad™ and Cabri Geometry™ allows one to manipulate dynamically the objects of elementary geometry, such as triangles and circles. Since the software will draw the trace of a moving object, one can also create and investigate many curves dynamically as well.
These curves provide students with an interesting set of applications of elementary geometry and also serve as concrete examples of concepts studied later in calculus and differential geometry.
The collection of curves that can be found in any handbook is very broad indeed. As examples of curves that can be studied with dynamic software, this paper will concentrate on the conic sections and curves related to them. Other examples can be found in [4].
Conics in Elementary Figures – the Parabola
Even in elementary geometrical figures, conics and other curves may be found hiding in the background.

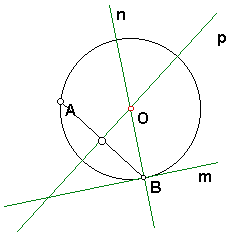
In this figure, a point A and a line m are given; B is a point on line m. A circle is constructed through A so that m is tangent to the circle at B. This is done by constructing the center point O as the intersection of the perpendicular bisector p of AB and the line n through B perpendicular to m.
Since this is dynamic geometry, it is natural to drag the given points A and B and see how O moves. If one drags A, then O simply moves along line n. But if one drags B, the center O traces a curve, a parabola. As B moves, O is always a point whose distance OA from A is equal to the distance from O to the line m, since this distance is OB. Thus the set of points O satisfies a standard definition of a parabola: the set of points equidistant from a point (the focus) and a line (the directrix).
Conics and Envelopes
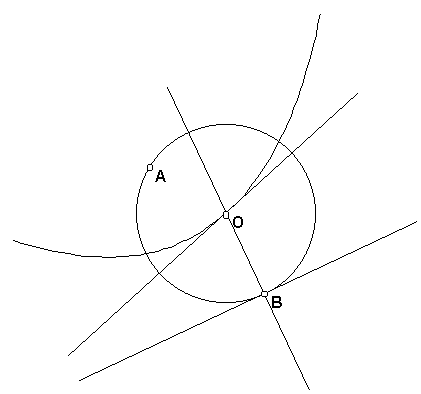
In the parabola construction above, the perpendicular bisector p always appears to be tangent to the parabola at O as B moves along m.
This leads to another way to view the construction – as an envelope of lines.
Begin again with point A in the plane and point B on line m. Construct the perpendicular bisector p of AB as before. Then trace line p as B moves to see a family of lines.

The parabola is the envelope of this family of lines. It is the curve whose tangents are the lines of the family.
Teaching Considerations
This example of a parabola described as a point locus and also as an envelope presents interesting opportunities for students to investigate the properties of parabolas and also for them to consider with elementary tools some topics such as envelopes and tangents.
It also raises some interesting teaching questions: What should students discover for themselves and how much should be explained directly by the teacher? Also, should this example be presented briefly or should one take the time to go some detail?
For example, we can pose such questions as these:
Software Features–Traces, Loci and Conics as Objects
Sketchpad and Cabri offer more than one way to draw the parabola in the example above.
First, each offers a Trace feature. If the point O is traced, the software simply leaves a mark on the screen where O passes as B is dragged. The line p can be traced the same way. The advantage of tracing is that one sees how the set is created by the moving point O; one sees which position of B correspond to which point on the trace. The disadvantage of tracing is that the trace is not dynamic. If point A or line m is moved, the trace does not move to correspond to the changing geometry but must be erased and redrawn.
A second method of drawing the set of points O forming the parabola is to use the Locus command. The draws the whole trace at once, without having to drag B, and the Locus is dynamic - it moves to the correct new position when the point A or the line m is moved. The drawback of the Locus is that it is something of a black box. One does not see step-by-step how the locus is drawn.
In teaching, even though using the Locus immediately seems more efficient, students seem to understand better if they first Trace to see how the locus is drawn and then apply the Locus command to see how the locus changes as the initial data change.
Finally, Cabri Geometry constructs conic sections as objects as well as loci. Given five points, in this case five points on the parabola, Cabri will construct the conic through the five points. This conic object has the advantage over a locus in that it can be intersected with other objects. To study the projective geometry of conics, for example, this feature is a great advantage.
Extension to Ellipses and Hyperbolas
The same ideas that led to parabolas can be extended to construct ellipses and hyperbolas.
If we begin with a point A in the plane and a point B on a circle m, then construct a circle through A and B which is tangent to m at B.
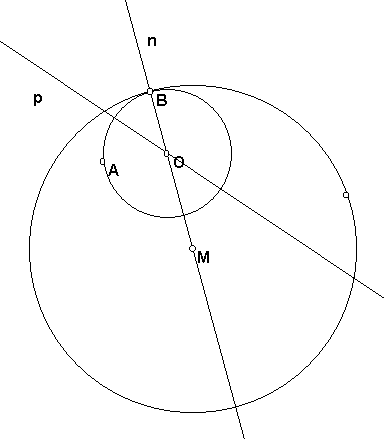
Drag point B around circle m and the center O will trace an ellipse if A is inside circle m and a hyperbola when A is outside circle m.
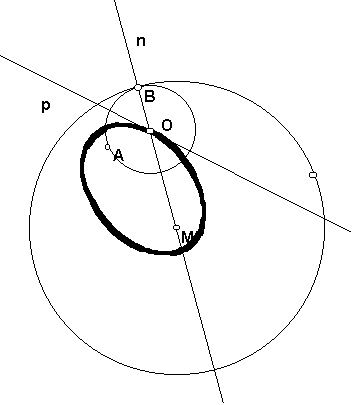
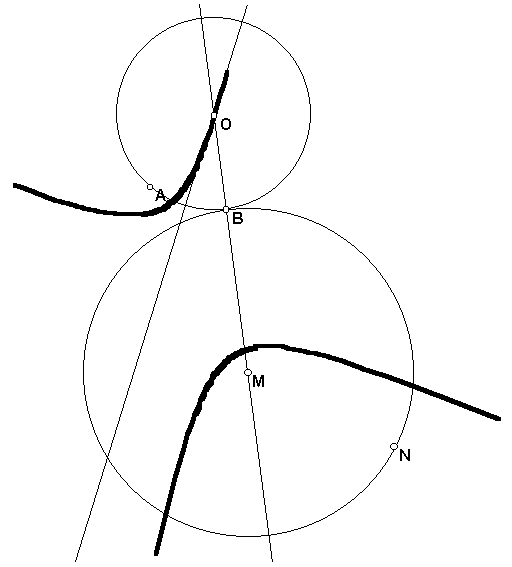
If the perpendicular bisector p is traced instead of the center O, again we obtain the conic as the envelope of a family of lines.
This method of constructing conics from a circle is called the Director Circle method.
Proofs, Other Tools and Optical Properties
The proof that the Director Circle construction does in fact construct an ellipse or a hyperbola uses a geometrical construction of a reflected billiard path or the reflection path of a ray of light.
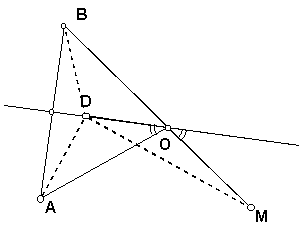
In the figure are given a line p and two points A and M on the same side of the line. Let B be the reflection of A across line p. For any point D on line p, the length of the path from A to D to M is the same as the path from B to D to M, since |AD| = |BD| and so |AD|+|DM| = |BD|+|DM|. Thus if we choose as D the point O which is the intersection of segment BM with p, then the path is shortest for this choice of D=O. The path from A to D to M is the path of a billiard ball or a light ray reflected from the line. It is clear from the figure that the angle of incidence equals the angle of reflection, as marked.
This figure appears in the Director Circle construction. In this case B is on the directing circle, which has center M and radius r, so for every choice of B, the point O satisfies |AO|+|OM| = |BO|+|OM| = |BM| = r. Thus given the points A and M, the set of point O is the set of points for which the sum of the distances |AO|+|OM| = r. This is the usual definition of an ellipse with foci A and M.
We see from this construction if a light ray from A is reflected from the ellipse (i.e., reflected from the tangent line) at any point O, then the reflected ray passes through M. This focusing property for light rays is why the points A and M are called foci of the ellipse.
Since the tangent line to the ellipse at O is part of the construction, given any point P, the reflected light ray from P to O can be constructed. Reflect the ray PO across the tangent line to get the reflected ray. (Remove the segment from P' to O so that the reflected ray begins at O.) For a given P, if the locus of reflected rays is traced, then if P is at one of the focal points, the lines come together, but otherwise the envelope of the rays is a caustic, a curve with cusps. Such a curve with cusps will appear as a curve of brightness when light is reflected in a cup of coffee. Such a curve is called a caustic {see [1]).
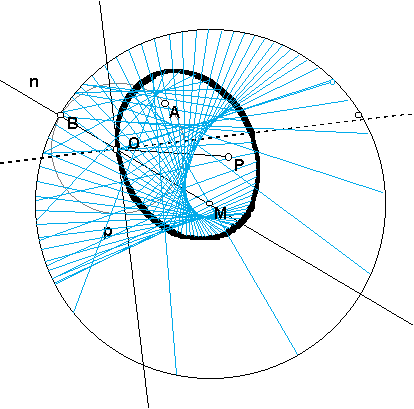
Other Constructions of conics
While computer software is very powerful, it is rather abstract tool. It is helpful for student learning to compare computer drawing with physical methods for drawing conics.
The Directing Circle construction of the perpendicular bisectors can be carried out conveniently by paper folding (the perpendicular bisector of AB is obtained by folding the paper so that A and B coincide.) If enough folds are made, the conic appears as the envelope of the lines. Another method uses a partially transparent plastic mirror (such as the Mira™) which allows one to draw a perpendicular bisector quickly by aligning the point B behind the mirror with the reflection of point A.
A better-known construction of an ellipse by hand uses two nails, one at each focus F and G, and a piece of string of length L tied at F and at G. A pencil pushed against the string at point P will trace the set for points for which |FP|+|PG|=L.
This construction can be simulated with dynamic software, by constructing a segment AB of length L and dividing it into two sub-segments AC of length L1 and CB of length L2. Then construct circles of radius L1 centered at F and radius L2 centered at G. The two points labeled P are the intersection points of the circles. When point C is dragged to change the lengths, the intersection points trace the ellipse.
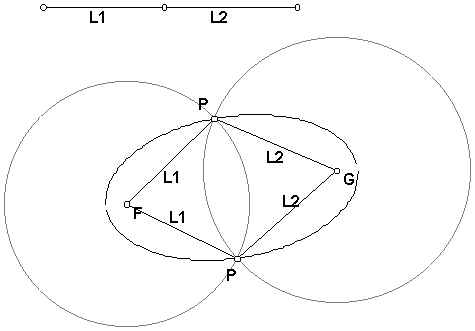
This simple construction is interesting to investigate, but it has some practical difficulties that make it less useful than the Directing Circle construction. The locus is really two loci, one for each intersection point P of the two circles; there is a gap between the two loci at the ends of the major axis. Also this construction does not construct the tangent lines, so that certain constructions that require the tangent line are not readily available.
The directing circle construction parametrizes the conic by a single-valued function of points on the circle, one point on the conic comes from each point on the circle. This latest construction parametrizes the ellipse by a segment, with two points of the ellipse for each value of the parameter (in coordinate geometry, this is a positive and negative square root).
Conic Sections and Cones – Dürer's Construction
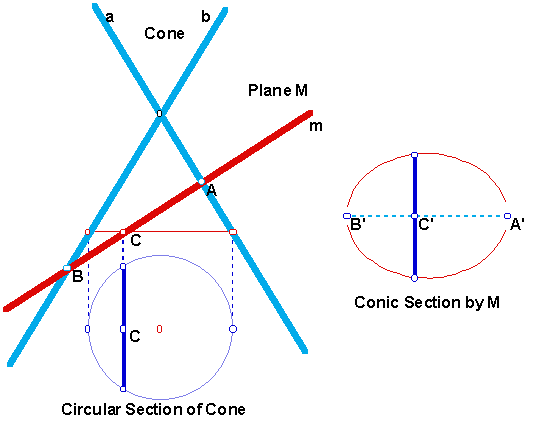
We have been referring to ellipses, parabolas and hyperbolas as conics, or conic sections. This name means that the curves can be defined as the intersections of a cone with a plane M. A construction of Dürer, based on the work of Apollonius, draws the plane curve from a cross-section of the cone and the plane (the cross-section is cut by a plane through the axis of the cone perpendicular to the plane M).
The cross-section of the cone looks like two intersecting lines, a and b, and the cross-section of M is a line m. Suppose that M intersects line a at A and line b at B.
If a point C moves along line m, the plane through C perpendicular to the axis of the cone cuts the cone in a circular section. This circular section intersects plane M in a segment perpendicular to line AB. The endpoints of the segment lie on the conic section. This segment is also a chord of the circular section and thus its length can be constructed from the circle.
The method of Durer was to plot a large number of points C on a segment of length AB and to construct the segment with C as midpoint and end points on the conic section.
This plot can be done well with software. The point C can be used to trace the locus and give an accurate figure that is also dynamic. If the line m is moved or if the lines a and b defining the cone are moved, then the conic section curve changes accordingly.
Without further details, here is a figure of this construction (see [4]).
This method uses some ideas of descriptive geometry in that plane figures from different planes are drawn to scale on a single plane, the plane of the computer screen.
Projective Construction of Conics
The construction of a curve as a conic section can be interpreted as constructing the curve as the central projection of a circle onto another plane (with the center of projection the center of the cone). A natural domain of geometry for the study of conics is projective geometry, for conics are projected to conics.
A famous theorem of the projective geometry of conics is Pascal's Theorem on inscribed hexagons. If P1, P2, P3, P4, P5, P6 are points on a conic, then these points are the vertices of a hexagon inscribed in the conic. The theorem of Pascal states that the opposite sides (extended) of this hexagon intersect in three points which are collinear. The line p containing these points is called the Pascal line.
This construction can be made and viewed with dynamic software, and some interesting limiting cases can be studied where certain vertices coincide and the side of the hexagon becomes a tangent to the conic.
However the construction can be reversed and used to construct a general conic through five given points.
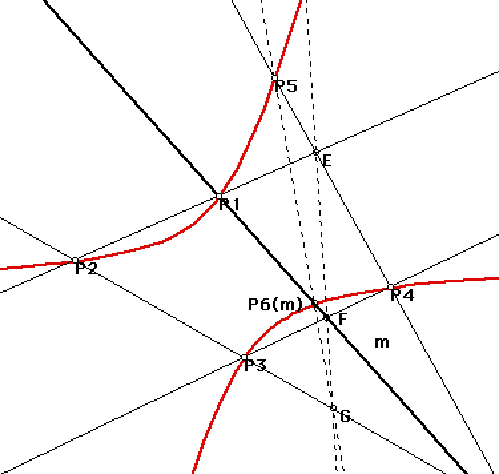
Given five points (now three of which are collinear), we plot the conic as follows. Let m be a moving line through P1; the Pascal theorem can be used to construct a point P6(m) on m which is also on the conic (since P1 is also an intersection point of m and the conic, this point will turn out to be unique).
The construction is just a process of sorting out what is known. Since line m will be a side of the hexagon P1P2P3P4P5P6(m), even through P6 is not yet known, there are enough sides to determine the Pascal line p as the line through the intersections E of P1P2 with P4P5 and F of P3P4 with m. Then the intersection G of p with the remaining side P2P3 gives a point which is also on side P5P6, so line P5P6 is line P5G. Then we define P6(m) to be the intersection of m with P5G.
The point P6 can be traced as m moves (m can also be animated to rotate around P1 to give a more dramatic effect).
There are other methods from projective geometry for constructing conics. For example, given a circle c1 (or other conic) for every point P on the plane, there can be constructed a line p1 called the polar of P. Given a line q, the pole Q1 can be constructed so that q is the polar of Q. This polar correspondence can be viewed as a projective transformation from the plane of points P to the plane of lines p (the space of lines is a plane in projective geometry). If we choose another circle c2, then we can start with a point P, transform it to the polar p1 in c1 and than transform p1 to its pole P2 in c2. This map F, the composition, from P to P2 is a projective transformation of the plane. If we transform a circle d, the image will always be a conic. The nature of the conic will depend on the circles c1 and c2 and also the position of the circle d. This is a very general way to transform a circle to a conic. (See [2].)
Affine Mappings of Lines and Rational Curves
Given a line through A and B, the standard affine parametrization of the line by the real numbers t is given by the formula S(t) = (1-t)A + tB, or equivalently, S(t) = A + t(B-A), where we think of this as displacement of point A by the translation vector t(B-A). We can also think of t as a coordinate of point S on the line, with t = AS/AB, a signed ratio. We will call t the affine coordinate of S with respect to A and B.
This affine parametrization can be carried out with dynamic software for geometry. We begin with a line PQ and a point T sliding on PQ. Let t be the affine coordinate of T on line PQ. Then, given points A and B, we use this ratio to define S(t) to be the dilation of point B with center A and ratio t. Then this means exactly AS(t) = tAB, so t is the affine coordinate of S on AB.
This relationship can be used for curve stitching. Suppose we are given three points A, B, C in the plane. Let E be the point on line AB with affine coordinate t with respect to A and B and let F be the point on line BC with the same affine coordinate. If we drag point E along line AB, F moves along BC with the same corresponding coordinate. Connect these points to get line EF. Then the family of lines EF forms an envelope. This figure can be constructed with thread by punching a number N of equally spaced holes along segment AB and segment BC and pulling the thread through corresponding holes.
This envelope turns out to be a parabola. The point on line EF that is the point on the parabola is the point G on line EF that has affine coordinate t with respect to E and F! This was known to Apollonius and can be proved by computing E and F and then G in terms of A, B, C and t using the parametrization formula.
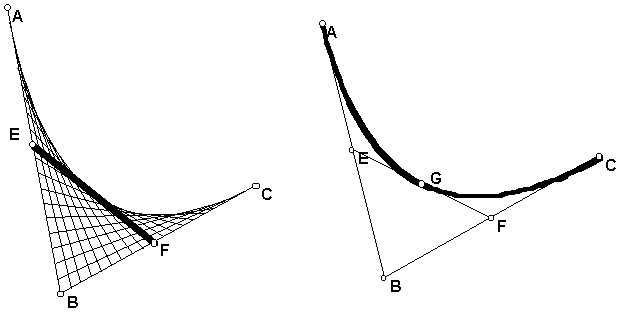
This construction is used in computer graphics for constructing piece-wise polynomial curves called spline curves. This is the construction of what is called a quadratic Bezier curve. The method of construction is called the de Casteljau algorithm.
A very useful curve in computer graphics is the cubic Bezier curve. The same algorithm using the same coordinate t constructs this, but it begins with four points and the construction is carried out one more step, as in this figure. (See [3].)
Affine Mappings of the Plane and Matrices
Ellipses occur as the images of the circle by linear or affine mappings. In (x,y) coordinates, such mappings are defined by linear functions F(x,y) = (ax + by +e, cx + dy + f). This expression can be written using vectors or matrices. Let P0 = (e,f), the image of the origin, and let P1 = F(1,0) = (a+e, c+f) and P2 = F(0,1) = (b+e,d+f). Then we can view F(x,y) equal the vector sum P0 + xM1 + yM2, where M1 is the vector P1-P0 and M2 is the vector P2-P0.
We can also think of M1 and M2 as the column vectors of a matrix. If P is the column vector (x,y), then F(P) = P0+MP. If we draw these vectors in the plane, we can construct F(P) for a point P and then study the images of simple figures such as rectangles and circles. These vectors can be drawn in the plane and manipulated dynamically with Sketchpad or Cabri. Then one can study the images of simple figures such as circles. In this figure P0 is the origin, so the function is F(P) = MP.
One can investigate many questions with such a figure. For example, one can discover that the ratio of the area of the image of a figure is a constant multiple of the area of the original figure and that this constant is the absolute value of the determinant. One can study special transformations such as shears, strains, rotations and reflections. On a more sophisticated level, one can study how the major and minor axes of the ellipse, which is the image of a circle, are related to the eigenvectors and eigenvalues.
Parallel Curves and Evolutes
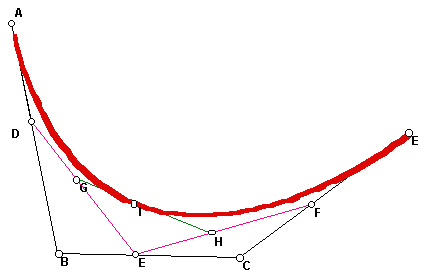
Given a curve such as a parabola, there are other curves and envelopes that can be constructed from the curve. For example, one can construct the parallel curves at distance d by constructing points P and Q on the normal line at O (the perpendicular to the tangent) which are at distance d from O. The parallel curves are the locus of P and the locus of Q as d varies. In the first figure is shown the locus of P for a small value of d.
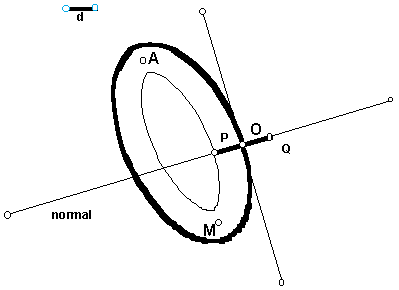
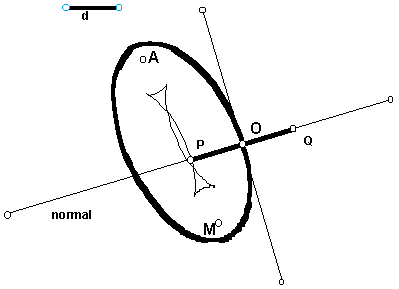
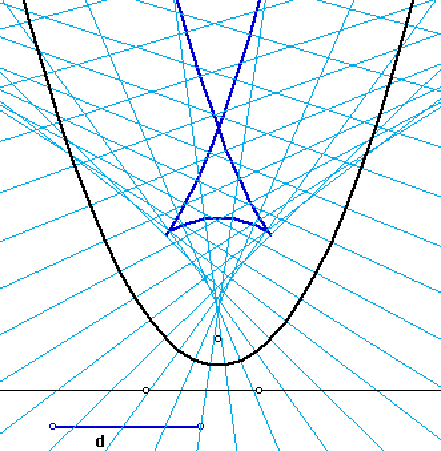
From this picture, one might conjecture that the parallel curve of an ellipse is an ellipse, just as the parallel curves of a circle are circles (except which d is equal to the radius). But in the second figure the parallel takes on a surprising shape with cusps for larger d. It is interesting to experiment and consider why the parallel curve has this shape. Some additional insight comes by considering the envelope of the normal lines, which is a curve called the evolute. One discovers that the cusps of the parallels lie on the evolute. Here is a parabola with the evolute shown as the envelope of the normal lines and a parallel curve with cusps on the evolute. (See [1].)
Bibliography