First steps to a geodesic dome

We have seen that any regular polyhedron can be inscribed in a sphere and thus the vertices create a regular tessellation of the sphere. In the plane, we know how to subdivide a triangular tessellation into a tessellation by similar triangles. On the sphere, things are a bit different. Suppose we have a triangle ABC, then the midpoint triangle A'B'C' is the triangle whose vertices are the midpoints of the sides of ABC.

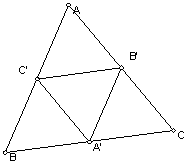
In the plane, all 4 small triangles are similar to ABC, so if ABC is equilateral, so are all 4 triangles.

On the sphere, let us take ABC to be a 90-90-90 triangle. So in coordinate space you can assume that A=(1,0,0), B = (0,1,0) and C = (0,0,1).

1. Find the coordinates of A', B', C'. These are the midpoints of the sides of the triangle ON THE SPHERE. Each of these points is distance 1 from the center (0,0,0) of the sphere.
2. The four triangles into which ABC is divided have 9 sides (some are shared). Find the Euclidean distances (measured as straight-line distance in 3-space) and also the spherical distances (measured in degrees or radians) of each of these edges. You will save yourself a lot of work by noticing which sides must be congruent.
3. Find the measure of all the angles in the figure.
4. Use the angle measurements to find the area of each of the 4 triangles, given that the sphere has area S.
5. Optional Extra Credit. Make a model from cardboard or straw of these four triangles (fastened together). Even better, make the dimensions so that it will fit exactly into a Lenart sphere. Or else, build your own spherical octant or even make 8 of these models from straws and fasten them together to form a polyhedron all of whose vertices lie on a sphere.