Math 487 Lab #4 - Conic Sections

Wed 1/28/04

Many ways of defining curves which turn out to be conics.

A. Ellipses and hyperbolas from distances

Definitions. Probably the most familiar geometrical definition of an ellipse (or a hyperbola) is in terms of the sum of distances to two points. We start with this.

• An ellipse with foci F1 and F2 (any two distinct points) is the set of points P so that the sum |PF1| + |PF2| = some constant k.
• A hyperbola with foci F1 and F2 (any two distinct points) is the set of points P so that the difference |PF1| - |PF2| = some constant k.

Note: The singular of foci is focus. The definition that we give of parabola is also about distance, but involves a special line called the directrix (there is also a defintion of ellipse and hyperbola that involves a special line also).

Experiment: Construction of ellipses and hyperbolas: a construction revisited from Lab 2.

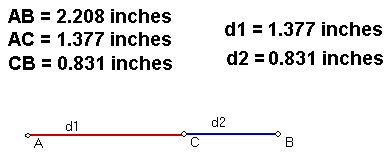
Set up the lengths and measures

• First we construct some segments that will provide the distances. In a new sketch, draw a LINE AB (NOT a segment) and construct a point C on the line.
• Hide the line and then construct segments AC and BC. Color them differently (say red for AC and blue for BC) and make them thick. Label segment AC as d1 and segment BC as d2.
• Measure the lengths of d1 and d2. Calculate the sum and difference of these lengths with the calculator. Also measure distance AB. Drag C to see what happens to the sum and difference.
• Observe: For what locations of C is the sum constant? For what location of C is the difference constant?

.

Construct two circles and trace the intersections

In the sketch, draw two points and label them F1 and F2.

Select segment d1 and point F1 and construct the circle c1 with center F1 and radius d1. Do the same for F2 and d2 to construct circle c2. Intersect the two circles and trace the two points of intersection G and H as you drag point C between A and B.

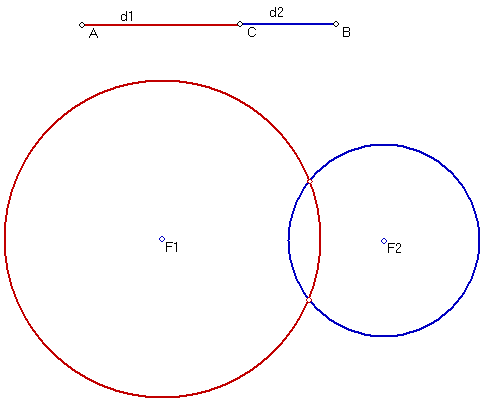
Experiment with a trace

• For some positions of the points F1 and F2, the trace of the points of intersection will be an ellipse. What locations of C on line AB trace points on the ellipse?
• For some positions of F1 and F2, a hyperbola is traced (note that both parts are traced). What locations of C on line AB trace points on the hyperbola?

Experiment with a Locus

• Turn off the tracing. Select G and C and Construct>Locus. Do the same with H and C.
• These loci form the same figure as the traces, but now it is possible to move F1 or F2 and watch the curve change dynamically. (When the figure is a hyperbola, if you want it longer, you can drag the endpoints.)
• What is true about F1 and F2 when the locus is an ellipse? What is true when the locus is a hyperbola? Why?

Questions A

1. Explain precisely why, when the trace appears to be some kind of oval, that the points G and H of the trace satisfy the definition of an ellipse. Tell what is the constant k and why.
2. Explain precisely why, when the trace appears to be some kind of unbounded curve with two parts, that the points G and H of the trace satisfy the definition of a hyperbola . Tell what is the constant k and why.
3. What are the relationships among F1, F2 and A and B that determine whether the trace is an ellipse or a hyperbola (or something else)? In other words, what data about these points are needed in order to predict whether an ellipse or a hyperbola is drawn? (And how do we make the prediction?) Explain your reasoning.

B. Distance Ratio — two points give Apollonian circle again

A review experiment with the same figure

• Hide the Loci and turn on tracing for G and H again.
• In the very same figure you have already constructed, make one more measurement. Use the calculator to compute the ratio d1/d2 (or measure this directly by selecting the two segments).
• Now instead of dragging C, drag point B. Notice that the sum and difference measures change, but this ratio measure remains constant.
• Observe the trace as B is dragged and the ratio is held constant. What is this familiar figure?
• Move C as near the midpoint as possible, so that the ratio is as close to 1 as you can make it. Now drag B again. What does the locus appear to be?

C. Distance Ratio — point and line case

We will continue by creating another trace, this time with the ratio of the distance to a point and the distance to a line being a constant. We can do it by making a few additions to our current sketch.

• First, use a Hide/Show button to hide the intersection points G and H. Select G and H and then create a Hide/Show button from the Edit ->Action Button menu.
• Next, construct the line (NOT SEGMENT) F1F2. Then construct the line through F2 perpendicular to line F1F2, and label this new line d.
• Next, construct the two lines parallel to d that are at distance d2 from d. You can do this by first constructing the points of intersection of line F1F2 with the circle c2. Then construct the lines through these two points parallel to d. Call these lines p1 and p2. The points on these two lines p1 and p2 are the points that are at distance d2 from line d.
• Now hide the line F1F1, the circle c2, and their points of intersection (make Hide/Show buttons if you want).

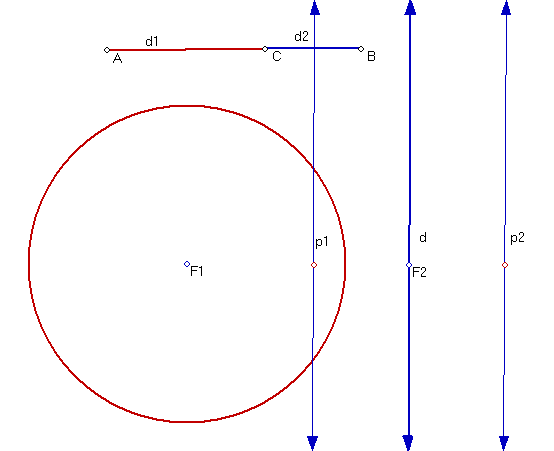
• Again, taking e = ratio d1/d2, any point of intersection Q of c1 and either line p1 or p2 satisfies the relation (distance Q to F1)/(distance Q to d) = e.
• Construct the two points of intersection of c1 with p1 and color them red. Also construct the two points of intersection of c1 with line p2 and color them blue. Trace all four points of intersection.
• Drag B to keep e fixed and to trace out the set of all such Q.

Definition. For this curve, the line d is called the directrix of the curve and the point F1 is called the focus. It is not obvious that this focus definition has anything to do with the other one, but it does.

Questions C

1. For what values of e do you get a trace that appears to be an ellipse? What values appear to give a parabola? What values appear to give a hyperbola? Consider that the ratio e tells the relative rate of growth of the radius of the circle and the half-distance between p1 and p2. Using this idea of rate of growth, explain for what ratios the circle will only intersect one line and when the circle will intersect both lines. Also you can explain what ratio will give a bounded figure and what ratio will give an unbounded figure.
2. If we wish to define the parabola as the locus above which is an unbounded locus but for which the circle only intersects one of the lines p1 or p2. Tell what value of e makes this true.
3. (Later) In the (x,y) plane, let the y-axis with equation x = 0 be the directrix and let F1 the focus = (p,0). Write down the ratio e in terms of coordinates and get an equation for the curve.

Note: The ratio e is called the eccentricity of the curve. These curves do turn out to be conic sections, but it is not obvious from this definition at all.

D. Parabolas and Circle Centers

(For D and E, see GTC, Investigations 1 and 2 of Exploration 6.4, pages 89-93, for more details. Also see Ogilvy.)

• In a new sketch, given a line (not segment) d and a point F, construct a (random) point X on d. Then construct the circle through F that is tangent to d at X. Let P be the center of this circle. Trace P as you drag X. What curve does this trace appear to be?
• Instead of tracing, turn off the trace of P and construct the locus of P as X varies.
• For any position of the point P, what is the relationship between the distance from P to F and the distance from P to d? Express this as a fact about the ratio e. Restate this relationship as a Definition of a Parabola.
• When you constructed P as the intersection of two lines, one of the lines p was the perpendicular bisector of XF. How does this line appear to be related to the parabola? Trace this line to see the parabola appear as the envelope of a family of lines.
• To confirm that this line p is a tangent to the parabola, we can see that for any other point Q on p other than P, the distance from Q to d is less than the distance from Q to F. Construct such a Q on p, and construct segments QF and QX. Why is QX greater than the distance from Q to d when Q is not P?
• Optical Properties of Parabolic Mirrors. Suppose a light ray hits a parabolic mirror at point P (a real mirror is obtained by rotating the parabola around the axis -- the line through F perpendicular to d). Then the light ray reflection is the same as the direction of reflection from the tangent line p at P. Show in your sketch that for a light ray perpendicular to the directrix, the reflected ray passes through F. In other words the light focuses at F. This is why F is called the focus.

E. Ellipses and Hyperbolas and Circle Centers

(See GTC, Investigations 1 and 2 of Exploration 6.4, pages 89-93, for more details. Also see Ogilvy.)

Experiment

• In a new sketch, given a circle d with center D and a point F placed anywhere inside d, construct a (random) point X on d. Then construct the circle through F that is tangent to d at X.
• Let P be the center of this circle. Trace P as you drag X. What curve does this trace appear to be?
• Instead of tracing, turn off the trace of P and construct the locus of P as X varies.
• Now drag F outside circle d. What happens to the appearance of the curve? What kind of curve does the locus seem to be now?
• When you constructed P as the intersection of two lines, one of the lines p was the perpendicular bisector of XF. How does this line appear to be related to the curve? Trace this line p to see the curve appear as the envelope of a family of lines.
• Compute the distances |PF|, |PX|, |DX|, |PD| and calculate |PF|+|PD| and also |PF|-||PD|.
• Look at the geometry and observe the measurements. When F is inside the circle and X moves, what quantities stay constant? What quantities are equal? How are these observations related to the definitions of ellipse and hyperbola at the beginning of this lab?
• When F is outside the circle, answer the same questions.
• Check that the line p is a tangent by the following calculator experiment (not a proof). Move F back inside d. An important relationship is that X is the reflection of F in p. We have seen the bent "reflection distance" |PF| + |PD| = |DX| = radius of d. Use the calculator to see that for any other point Q on p other than P, the distance sum |QF| + |QD| = |QX| + |QD| > |DX| when Q is not P. (This is true because QXD is a triangle.) Thus line p only intersects the curve at P, which is the only point where this inequality becomes an equality. Similar reasoning works for the hyperbola case.
• Optical Properties of Elliptic Mirrors. Suppose a light ray hits an elliptic mirror at point P (a real mirror is obtained by rotating the curve around line FD). Then the light ray reflection is the same as the direction of reflection from the tangent line p at P. Show with thick segments in your sketch that a light ray from D to P reflects to a ray through F. Thus light rays from one focus all reflect and focus at the other focus. Hyperbolas also have an optical property. Can you find and describe it?

Questions D

1. Study the geometry when F is inside the circle and explain why the points P satisfy the definition of an ellipse. (The calculator results are not an explanation, they are an illustration.)
2. Study the geometry when F is inside the circle and explain why the points P satisfy the definition of an hyperbola. From the geometry, tell what lines are the asymptotes of the hyperbola.
3. When F is inside the circle, explain why the line p only touches the locus of P at one point. This means giving a geometrical justification for the calculator experiment above.
4. For the ellipse case (when F is inside the circle) explain why the line p is the exterior angle bisector of angle FPD. What can you say in a similar vein for the hyperbola case?

Addendum: Circles tangent to 2 circles

This is a link to a rough GSP file with constructions and loci of circles tangent to 2 circles, as discussed in lecture.

Return to Math 445 Home Page.