Coordinate Systems in 3-Space
Background from the plane
To construct a coordinate system for 3-space, let us first
consider what we have used on the plane. 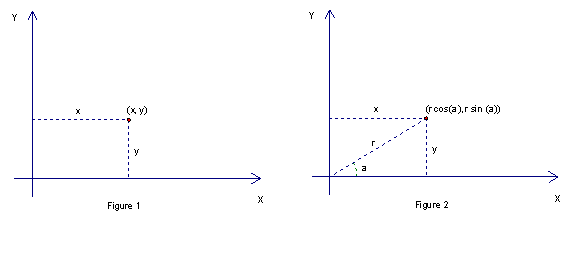
In figure 1, we see the traditional way of representing the location of points on a plane using a set of perpendicular axes. In figure 2, however, we see that there is another way of representing the location of an arbitrary point using the distance from the origin, r, and the angle between the x-axis and a line from the origin to the point in question. The x and y coordinates are, in fact, related to r and this angle, a, in the following ways:
cos a =
x/r, sin a = y/r, tan a = x/y, and x2 + y2 = r2.
Therefore, we can write the coordinates of a point P as (x, y) or (r cos a, r sin a), and move from one method of representation to the other easily using the aforementioned formulas.
Cylindrical coordinates
When moving into the realm of 3-space, we again have multiple ways of representing the location of a particular point. One obvious possibility would be to simply add another axis and use a “z” coordinate to take care of the added dimension (illustrated in Figure 3). Another possibility, however, is to use the same reasoning as before on the x-y plane (using an angle and distance from the origin), and use a height (i.e. the z coordinate) to represent the distance above or below the x-y plane (see figure 4).
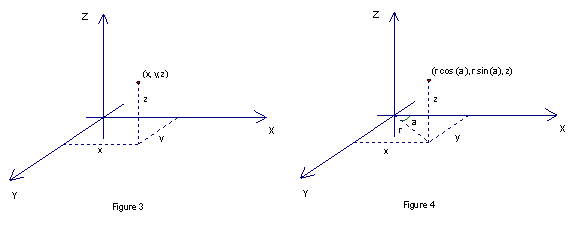
In figure 4, the same relationships hold true as in figure 2.
cos a =
x/r, sin a = y/r, tan a = y/x, and x2 + y2 = r2
Example:
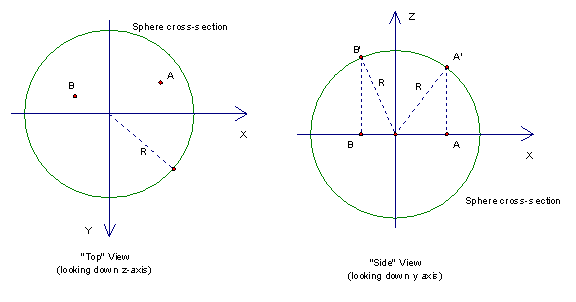
Let us use this new system to try and describe points on the
surface of a sphere in which the equator is the great circle that lies on the
intersection of the sphere of radius R with center (0,0,0)
and the x-y plane. Let A and B be points on the x-y plane such that A and B are
contained in the circle with equation x2 + y2 = R2 (the
equator). We now wish to find the cylindrical coordinates of A’ and B’ which
are the vertical (parallel to z-axis) projections of A and B on the sphere
respectively.
To see a way to solve this, look at a cross section cut by a plane thru one of the points and the origin (see figure 5). The z-coordinate of A’ can be easily found using the distance AO, where O is the origin, and the radius of the sphere, R.
zA’2 = R2 – OA2
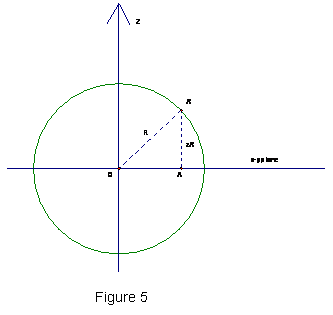
The same method, in fact, can be used to find the height of B’ above the x-y plane and we get zB’2 = R2 – OB2.
So we can locate any point on the sphere of radius R using cylindrical coordinates quite easily. Instead of (x, y, z) we use (r cos a, r sin a, R2-r2) where r is the distance from the origin, parallel to the z = 0 plane, and a is the angle made with the x –axis as described before. We also note that x2 + y2 = r2 and tan a = y/x.
Spherical
Coordinates
Another way of representing
points on a sphere is using spherical coordinates. This involves locating a
point using the radius of the sphere, R, the angle made on the z = 0 plane , a (as before), and the angle made the z-axis, b. A
diagram of this method is produced below.
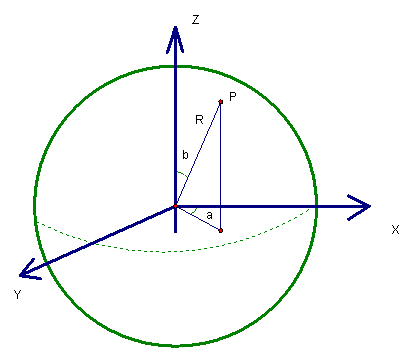
In this picture we see that x = R cos (a) sin (b), y = R sin (a) sin (b), and z = R cos b.
Also, tan a = y/x and x2 + y2 + z2 = R2. For example, let us locate the point at which the x-axis intersects the sphere. This occurs when b = 90 and a = 0. The coordinates of this point are therefore,
(R cos
0 sin 90, R sin 0 sin 90, R cos 90) = (R(1), R(0), R(0)) = (1, 0, 0), which is exactly what we
would expect.