I. Experimenting with the hyperbolic plane.
Drawing two seemingly parallel lines with a straight edge onto the hyperbolic plane, the lines actually look as though they are diverging.
II. Spherical vs. Hyperbolic
Spherical Hyperbolic
There are no parallels, lines diverge
They eventually intersect
III. Angular defect
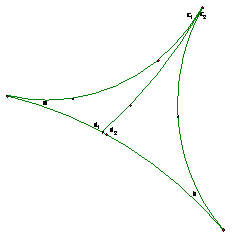
Defect of ∆ABC = 180 - (a + b + c)
Defect of ∆ACD = 180 - (a + d1 +c1)
Defect of ∆BCD = 180 - (b+ d2 + c2)
D of ∆ACD + ∆BCD = 360 – (a + b + c1 + c2 + d1 + d2)
= 360 – (a + b + c + 180)
= 180 – (a + b + c)
= D of ∆ABC
The angular defect of the big triangle is the sum of the defect of the smaller triangles. Thus angular defect is additive. Moreover, the bigger the triangle, the bigger the angular defect. And there are no similar triangles in this geometry—only congruent triangles.
We can also measure area in terms of angle defect, just as we did with angle excess (spherical excess).
IV. Review the parallel postulate of Euclidean geometry:
We used the side, angle, side similarity of a triangle to prove angle sums of a triangle equal 180.
The parallel postulate proves: SAS, existence of non-defective triangles, existence of rectangles, and midpoint triangle similar to the big triangle.
If there is a straight line and segments perpendicular to this line of equal lengths, then to the tops of the perpendiculars form a straight line?
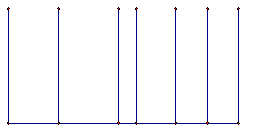
Euclidean: Yes
Spherical: No
Hyperbolic: No
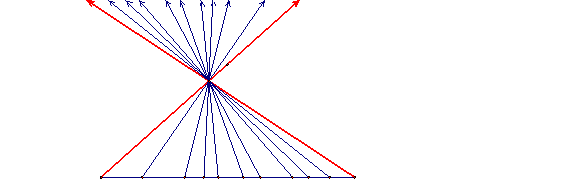
The red lines are limiting-, critical-, asymptotic-parallels. Note that as the intersection point moves close, the angle of parallelism gets bigger, and as it moves farther away, the angle of parallelism smaller.
V. Rectangles
The existence of a non-defective triangle proves the existence of a rectangle:
You can construct the altitude of a non-defective triangle and have a non-defective right triangle. Then putting two non-defective right triangles together, you will have a rectangle. And you can put as many rectangles together as you’d like to get an arbitrarily large rectangle.
Reference problems 2 and 5 from Sved chapter 4.
VI. Poincare
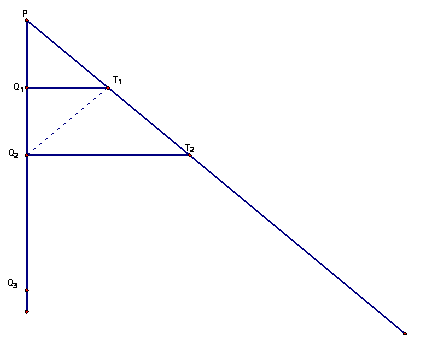
Let Q1T1 be the perpendicular bisector
of PQ2. Then ∆PQ1T1
= ∆Q2Q1T1 and the defect of ∆ PQ2T2
is at least twice that of ∆PQ1T1. The defect of ∆PQ3T3
is at least twice that of ∆PQ2T2 and so on. The defect is at least doubled every time,
but the defect must also be less that 180, so this is a contradiction. Thus there will be the case such that line PT1 and the
perpendicular at Qn do not meet—and they will be ultra parallel.