T is a “triangle” created by the intersection of three great circles.

How do you find the area of T on a sphere of area S?

T + U[a] = (a/360°)S T + (U[a] + U[b] + U[c]) = S/2

T + U[b] = (b/360°)S U[a] + U[b] + U[c] = S/2 - T

T + U[c] = (c/360°)S

3T + (U[a] + U[b] + U[c]) = ((a+ b + c)/360°)S

3T + (S/2 - T) = ((a + b + c)/360°)S

2T = ((a + b + c)/360° -1/2)S

T = ((a + b + c - 180°)/360°)S/2 a + b + c - 180° = έ = “spherical excess” (in degrees)

T = έ(S/720°) S/720° is a constant

Area is directly proportional to spherical excess.

Girard’s Theorem (or special case of Gauss-Bonnet)

T = έL

How do you find the “mystery constant” L?

Look at a hypothetical case where the three angles of the triangle T are all 90-degrees.

So the spherical excess έ = 90° + 90° + 90° -180° = 90°.

You know that T = S/8, because the sphere is cut into 8 congruent figures of T.

Now S/8 = 90°L and L = S/720°

Spherical Excess in a Quadrilateral

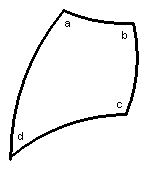a + b + c + d = 360°

or (a + b[1] + d[1]) + (c + b[2] + d[2]) = 360°

So έ = (a + b[1] + d[1]) + (c + b[2] + d[2]) - 180° - 180°, and έ = έ[1] + έ[2].

For a square in a sphere, έ = 4(120°) - 360° = 120°

So the area is (120°/720°)S = S/6

Review the “dot” operand for the homework/midterm: x·y = |x||y|cosθ