Trios of tangent circles from 3 centers

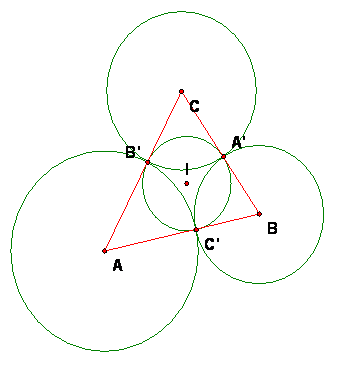
Let ABC be a triangle. Construct the incenter I as the point of concurrency of the interior angle bisectors and the incircle with this center. The radii IA', IB', IC' are all perpendicular to the sides.

These segments now divide the triangle into 3 quadrilaterals, such as AC'IB'.

The quadrilateral AC'IB' has right angles at B' and C'. I is equidistant from lines AB and AC, so I is on the bisector of angle C'AB' (of course we constructed I that way, but we can also see it starting with this figure).

As we have proved before the two tangent segments AC' and AB' are congruent.

Thus AC'IB' is a kite with two right angles (we can call it a "right kite" for fun). By the carpenter locus theorem, this right kite is a cyclic quadrilateral that can be inscribed in a circle with diameter AI.

Both of the other two quadrilaterals BA'IC' and CB'IA' are also right kites.

But since the segments AC' and AB' are congruent and the angles at C' and B' are right angles, the circle with center A through C' also passes through B' and this circle is orthogonal to the incircles. The same is true for the corresponding circles with centers B and C.