The Circle Pencil Story

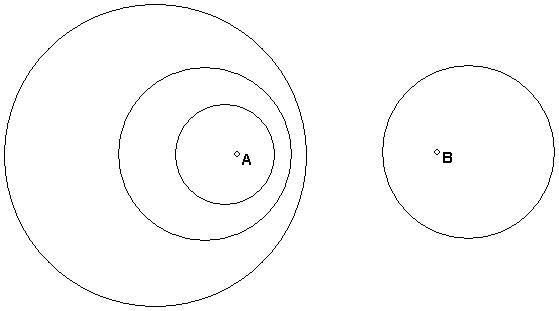
Apollonian circles are defined by ratio of distances = constant.  This means that the line AB intersects an Apollonian circle in points C and D that divide AB harmonically (just the definition of harmonic division. CD is a diameter of the circle.

Inversion of a point in at circle is intimately related to orthogonality of circles.  If P is inverted in circle c to get P', then any circle d through P and P' is orthogonal to c.

A calculation shows that inversion is related to harmonic division.  The line through the P and the circle center cuts the circle at points A and B.  Then P and P' divide AB harmonically.

Putting this all together we get important relations:

• Every circle (and line) through AB is orthogonal to every Apollonian circle of A and B (including the perpendicular bisector of AB as a circle also).
• For every point P distinct from A and B, there is exactly one Apollonian circle of A and B through C and exactly one circle through A, B, and C (including the two lines as circles as explained above).

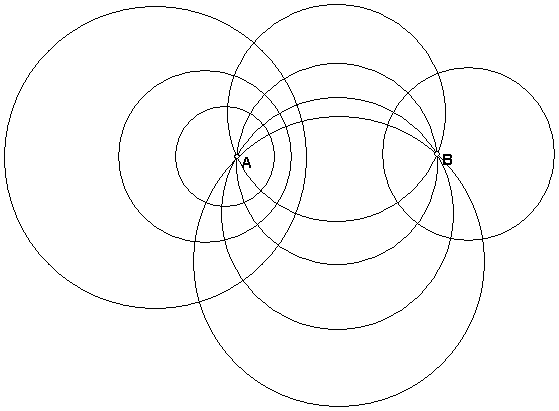
We call the set of all circles through A and B (including line AB) the elliptic pencil of circles through A and B.  We call the set of all Apollonian circles (including the perpendicular bisector of AB) the hyperbolic pencil defined by A and B. The set of all circles orthogonal to the circles of an elliptic pencil is a hyperbolic pencil, and vice versa.

If A and B get very close we get close to a limiting case, called a parabolic pencil.  These are a set of circles through A and all tangent to the same line at A (the pencil includes the tangent line.  The set of all circles orthogonal to the circles of a parabolic pencil is a parabolic pencil.

How to Construct this picture

Suppose a figure contains part of this picture. How can the rest of the points and circles be constructed?

For example, suppose that two disjoint circles c1 and c2 are given. How can the points A and B be constructed so that c1 and c2 are Apollonian circles of A and B?

• Construct any two circles d1 and d2 orthogonal to c1 and c2. (In fact, one of the "circles" can be the line of centers of c1 and c2.) The intersection of d1 and d2 will be A and B. Then any circles through A and B will te orthogonal to c1 anc c2. Likewise any circle c orthogonal to d1 and d2 will be an Apollonian circle of A and B.

If the points A and B are given, then one family (pencil) of circles is the family of circles through A and B whose centers are on the perpendicular bisector of AB. The other family can be constucted as circles orthogonal to these circles or by the Apollonian circle constructions from ratios, especially the one that uses the angle bisectors of a triangle. (See Ogilvy.)