Geodesic Sphere Answers
Suppose one face of a regular octahedron is divided into 9 equilateral triangles. Each of the triangles in the plane is also equilateral.
Vertices in the plane
The vertices of the original triangle are
(1, 0, 0), (0, 1, 0) and (0, 0, 1).
The vertices of the sides divided into thirds are
(0, 2/3, 1/3), (0, 1/3, 2/3), (1/3, 0, 2/3), (2/3, 0, 1/3), (2/3, 1/3, 0), (1/3, 2/3, 0),
and the vertex in the center is (1/3, 1/3, 1/3).
Vertices on the sphere
The vertices of the original triangle projected to the sphere are
A = (1, 0, 0), B = (0, 1, 0) and C = (0, 0, 1).
The vertices of the sides divided into thirds are
A1 = (1/sqrt5)(0, 2, 1), A2 = (1/sqrt5)(0, 1, 2),
B1 = (1/sqrt5)(1, 0, 2), B2 = (1/sqrt5)(2, 0, 1),
C1 = (1/sqrt5)(2, 1, 0), C2 = (1/sqrt5)(1, 2, 0),
and the vertex in the center is M = (1/sqrt 3)(1, 1, 1).
Spherical Lengths of Segments
This figure represents what happens when the triangles are projected from the center to the surface of the sphere circumscribing the octahedron. ALL SEGMENTS THAT ARE DESCRIBED BELOW ARE THE SPHERICAL SEGMENTS NOT THE PLANAR ONES. The picture is not a realistic picture of the spherical figure. The labeled points are the ones listed above.
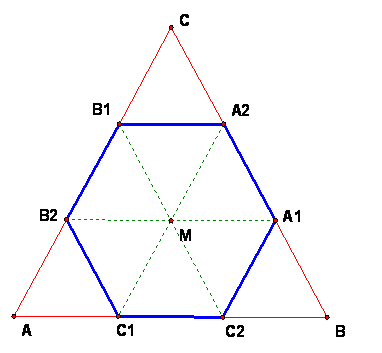
Spherical Length of segments
For any of the labeled points above, if the points are P and Q, then the cosine of the spherical distance from P to Q is just the dot product of OP and OQ (since the lengths |OP| = |OQ| = 1).
We compute some distances below
|
Pt P |
Pt Q |
Dot product = cosine of spherical distance P to Q |
spherical distance P to Q in degrees |
spherical distance P to Q in radians. |
|
A = (1, 0, 0) |
C1 = (1/sqrt 5) (2, 1, 0) |
2/sqrt 5 |
Red segment r = 26.56505 |
0.463648 |
|
C1 = (1/sqrt 5) (2, 1, 0) |
C2 = (1/sqrt 5) (1, 2, 0) |
4/5 |
Blue segment b = 36.8699 |
0.643501 |
|
C1 = (1/sqrt 5) (2, 1, 0) |
B2 = (1/sqrt 5) (2, 0, 1) |
4/5 |
Blue segment b = 36.8699 |
0.643501 |
|
M = (1/sqrt 3) (1, 1, 1) |
C1 = (1/sqrt 5) (2, 1, 0) |
(3/sqrt 15) = sqrt (3/5) |
Green segment g = 39.2315 |
0.68472 |
Notice that in the
table, the two red segments C1C2 and C1B2 are congruent.
Since reflection in the 3 perpendicular bisectors of the
triangle ABC carry a segment to a congruent segment, we can check that every
segment in the figure is reflected to one of the segments in the table, so the
table of lengths is complete.
All the blue segments
are congruent, all the dashed green segments are congruent, and all the red
segments are congruent.
All triangles congruent to two spherical triangles
From SSS and the remarks above, we see that the 9 triangles are each congruent to one of two triangles,
- the "corner isosceles right triangle" AC1B2 with sides blue-red-blue and
- the "hexagon sixth triangle" MC1C2 with sides green-red-green. (Since all the angles at M are congruent, and there are 6 angles, each angle at M = 60 degrees.)
Angles in the spherical triangles
Corner triangles
For the triangle AC1B2, it is already known that angle A = 90 degrees and also angle C1 = angle B2 by isosceles.
For angle AC1B2, the sides are great circles with plane equations
z = 0 and -x + 2(y + z) = 0
whose normal vectors are
(0,0,1) and (-1, 2, 2).
The cosine of the angle = dot product of normal vectors divided by the product of the lengths:
cosine of spherical angle AC1B2 = 2/sqrt(9) = 2/3.
So, angles of this triangle are
|
|
A |
C1 |
B1 |
|
Degrees |
90 |
48.18969 |
48.18969 |
|
Radians |
1.570796 |
0.841069 |
0.841069 |
Hexagon Triangles
As was observed before, angle M in spherical triangle MC1C2 = 60 degrees, and also angle C1 = angle C2 by isosceles.
.
To find angle MC1C2, we can find the equations of the planes of the great circle sides.
- Great circle C1C1 has equation z = 0 and normal vector (0, 0, 1) again.
- Great circle MC1 has equation x – 2y + z = 0, with normal (1, -2, 1).
Then use the dot product divided by lengths to get cosine of the angle:
cosine of spherical angle MC1C2 = 1/sqrt(6)
So, angles of this triangle are
|
|
M |
C1 |
C2 |
|
Degrees |
60 |
65.90516 |
65.90516 |
|
Radians |
1.047198 |
1.150262 |
1.150262 |