Group Assignment. Problem 5.

Text and figures by John Munchak. Proofed by Lana Kim.

Explain with proofs why the inversion of a line or a circle is a line or a circle. Describe how these results can be unified by adding a point at infinity. Show how to construct the image of a figure made of two circles c and d through points A and B and circles e and f orthogonal to c and d, when the figure is inverted in the circle with center A though B.

First it may be helpful to define what inversion is.

The inversion of a point P in a circle with center O and radius r is the unique point P' on ray OP in which OP' = r²/OP.

For example, for a point P inside a circle with center O:

Construct ray OP and the perpendicular at point P. Where the perpendicular intersects the circle are points A and B. Construct radii from center O to A and B. Construct tangents at points A, B by constructing perpendiculars of the radii at points A, B. The tangent at A intersects at point P' on ray OP (and the tangent at B intersects at point P' as well).

We shall prove that triangle OPA is similar to OAP'. Angle OPA and OAP are right angles by construction, and angle P'OA is the same AOP. So by the Angle-Angle theorem, triangles OPA and OAP' are similar, so OA/OP = OP'/OA. So, knowing that OA is the radius r, multiply to get OP' = r²/OP.

Intuitive Inversion

So we know the inversion of a point through a circle I is a point. A point on the circle of inversion inverts to itself, and this can be checked by using OP' = r²/OP. A point inside the circle of inversion I not on the center inverts outside the circle and vice versa. A point very close to the center of I inverts to a point very far away from the circle, and this can be checked with OP' = r²/OP, because if OP is very small in the denominator, OP' will be very large. The closer a point approaches the center, the closer its inverse approaches infinity. So a point at the center of I inverts to infinity.

So what does the inversion of a line look like? A line that does not intersect I inverts to a circle inside I and passes through its center. This makes sense because the line extends to infinity and the center of I inverts to infinity. If a line intersects I but does not pass through its center, it inverts to a circle passing through the center, though the line's intersection points invert to themselves. If a line intersects the center of I, the image of its inversion appears to be the line itself, though technically only the two points of intersection with I map onto themselves. A circle not passing through the center of I inverts to a circle.

The second part of the problem may help illustrate

Show how to construct the image of a figure made of two circles c and d through points A and B and circles e and f orthogonal to c and d, when the figure is inverted in the circle with center A though B.

Start with two circles c and d that intersect each other at points A and B. (Or, if you prefer, start with points A and B and place two random points R1 and R2 and construct two circles c and d through points A, B, R1 and A,B, and R2.)

Construct two circles e and f that are orthogonal to both c and d. The centers of e and f must be on the radical axis of c and d. The radical axis of c and d passes through A and B, the points of intersection. So pick a point P1 on the radical axis to be the center of your first circle orthogonal to c and d. Find the midpoint M1 of the segment between P1 and the center of c. The circle centered at M1 with radius M1P1 intersects c at the points T1 and T2. T1 and T2 are the points where the two tangent lines to c through P1 exist. The circle e centered at P1 and radius P1T1 is orthogonal to c and d.

(See figure).

Repeat the same method for another point P2 to get circle f, which will also be orthogonal to c and d. (See figure below.)

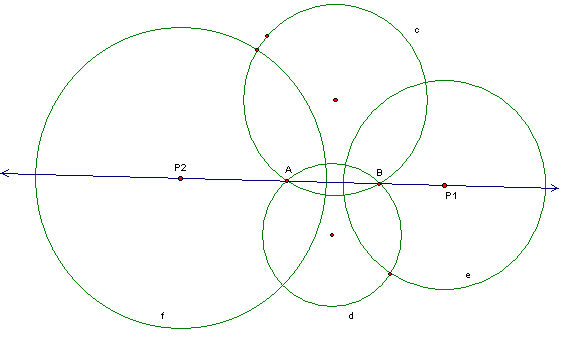
By the way, c and d are part of the Elliptic (2-point) pencil of circles; e and f are part of the Hyperbolic (zero-point) pencil of circles, or Apollonian circles.

Now we need to add a circle of inversion to our figure. Our circle of inversion will be centered at A and pass through B.

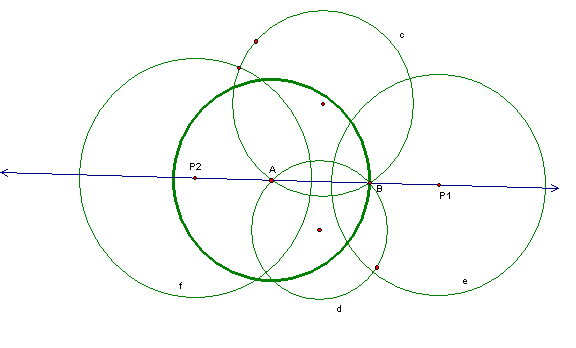
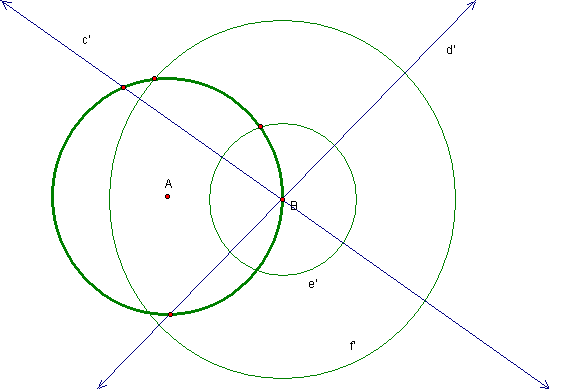
Let's see what happens when we invert circles c and d first.

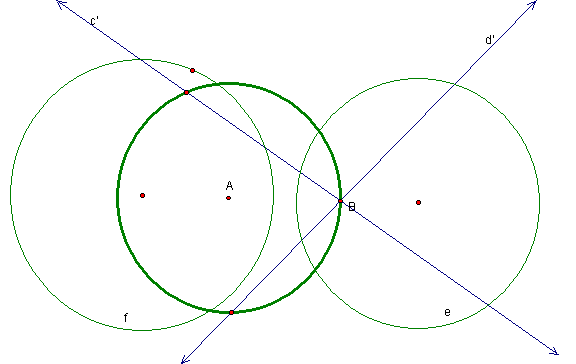
Since c and d passed through the center of the circle of inversion, they invert to lines. The lines c' and d' are fairly easy to construct: for each, simply draw a line through the two points where the original uninverted circle intersected the circle of inversion.

In order to invert e and f, we must keep in mind that the inversions of e and f must remain orthogonal to the inversions of c and d, since angles are preserved in inversion. It is also useful to note that circles e and f do not pass through A, the center of the circle of inversion, so they will invert to circles.

For e', we know two of the points that lie on e' are the same two points where e intersected the circle of inversion. Also, we know that for e' to be orthogonal to both c' and d', its center must be B, the intersection of c' and d'. This makes sense because a line orthogonal to a circle must pass through the circle's center. The same logic follows for f'. (See figure below.)