Inversion has many important properties when dealing with circles

Group Assignment Two — Group 1 Written by: Anna Lodahl

February 6, 2004 Proofread by: Joel Adriance

Caitlin McNamara

Inversion has many important properties when dealing with circles. One of these properties is that when there is a point A inverted to point A’ any circle that goes through these two points will be orthogonal to the inversion circle. In order to understand this one must know the definition of inversion and orthogonal circles, and some about equal secant lines from an identical point outside an arbitrary circle. From these the Pythagorean Theorem will be used to prove that in fact any circle through points A and A’ is orthogonal to the inversion circle.

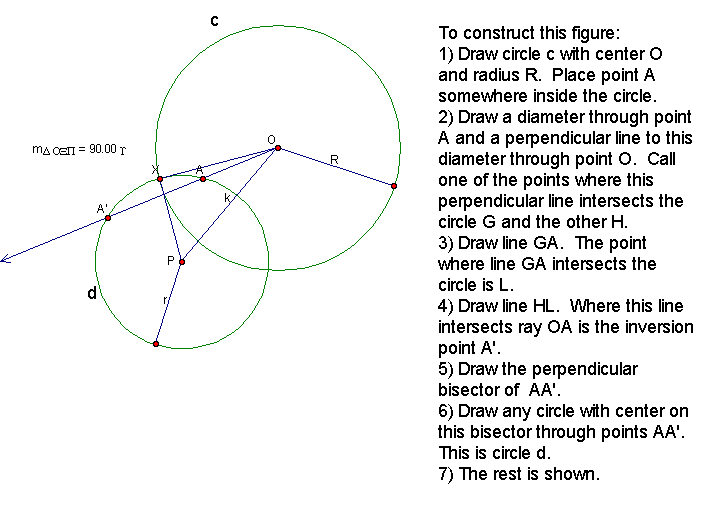
What does inversion mean? Take an arbitrary circle c with center O and radius R and invert a point A to get A’. If one of these points (either A or A’) is inside the circle the other will appear outside. The point A’ will be on ray OA with (OA’)(OA) = R². There are many methods to determine where the inversion point A’ will be on this ray. By definition the words orthogonal, normal, and perpendicular all mean the same thing: an intersection of 90 degrees. So when two circles are orthogonal, one of their intersections must have tangents to the circle at this point (they must intersect in two points for orthogonality to hold, otherwise they would be tangent) that are perpendicular. That is, they must meet at 90 degrees. As for the other intersection, it makes sense and one is able to prove that it must be a 90 degree intersection as well.

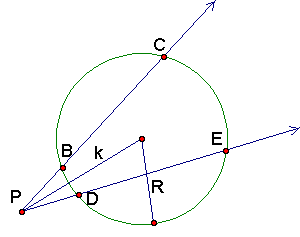
With the definitions out of the way there is only one more thing to understand before putting everything together. Any two secants through a circle from a common point outside the circle have equivalent products of their segments. That is, when there are two secants to a circle from point P through points B and C, and also points D and E, (PB)(PC) = (PD)(PE). If the distance from point P to the center of the circle is k it can be shown that this expression is also equal to (k — R)(k + R) with R being the radius of the circle. See figure on next page.

To make use of the tools just discovered in the previous two paragraphs take the arbitrary circle c defined above with center O and radius R (see figure on next page). Also make a circle through points A and A’ and call it d with radius r and center P. One point where this circle intersects circle c is point X. Using the secant correlation think of the point O as the point outside circle d with the secant points A and A’ going through d. The segment OP represents k shown above. The following should now be easy to see:

(OA)(OA’) = (OP — r)(OP + r) = R² (by definition of inversion)

(OA)(OA’) = (OP)² — r² = R²

(OP)² = R² + r²

(OP)² = (OX)² + (PX)²

Note: OX is the radius of circle c which equals R.

PX is the radius of circle d which equals r.

Triangle OPX as shown in the figure is a right triangle with hypotenuse OP (think about the Pythagorean Theorem). At this point the radii are perpendicular, hence that tangents are as well, so the circles must be orthogonal. Remember that the intersection we chose to put X in was arbitrary. This same reasoning works for a point Y placed at the other intersection. If two circles are orthogonal in one of their intersections they are orthogonal in both.

This shows that any circle through points A and A’ must be orthogonal to the inversion circle c.