
A. Given points A and B and a constant k > 0, use algebra to prove that there is exactly one point C in segment AB so that |AC/BC| = k. Find the value of t, so that the point C = (1-t)A+tB.
Answer
We know AC/CB = t/(1-t). Since C is between A and B, the signed ratio AC/BC < 0. So AC/BC = -k = - t/(1-t). Solving the equation k = t/(1-t) we get
k(1-t) = k -kt = t, so t = k/(1+k) and 1-t = 1/(1+k).
C = ( k/(1+k))A + (1/(1+k))B.
B. Given points A and B and a constant k > 0, use algebra to prove that there is exactly one point D in on line AB but not in segment AB so that |AD/BD| = k. [This is true except for one special case of k. What is this k?] Find the value of t, so that the point D = (1-t)A+tB.
Answer
We still have AD/DB = t/(1-t), but AD/BD = +k. Thus we get -k = -AD/BD = -AD/DB = t/(1-t). Solving, we get t = -k/(1-k) and 1-t = 1/(1-k).
D = ( -k/(1-k))A + (1/(1-k))B.
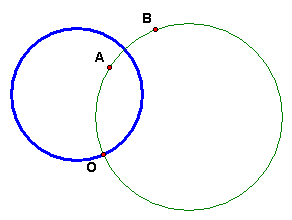
This figure is a line in Dr. Whatif's Euclidean geometry.

Using this figure, or a close facsimile, make two constructions.
Construct m and explain your method. (The D- perpendicular bisector of AB is the D-line m so that the D-reflection of A is B.
The circle looks like this. It must pass through O and, since it is orthogonal to the circle c through O, A, B, it is orthogonal to the circle at O.
To construct the D-perpendicular bisector as a Euclidean circle, we construct the Euclidean center E. Snce te circle is orthogonal to c at O, the center E of the circle is on the tangent line to c at O. Also, since the inversion of the point A in the circle with center E is B, then A, B and E are collinear. Thus E is the intersection of the tangent line to c with the Euclidean line AB.
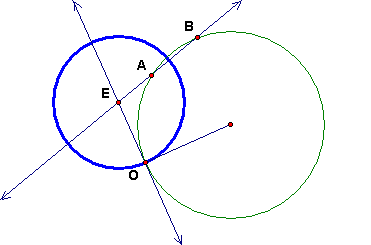
(Another way of thinking about it is this. Let d be any othe circle through AB. Then we are constructing the circle that is orthogonal to c and d passing through O. This is the 1 point + 2 circle construction that we have seen before.)
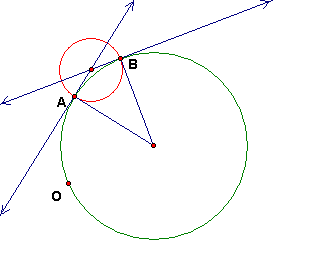
Construct the D-circle with diameter AB and construct its D-center. Again, explain your reasoning.
The circle is orthogonal to circle c at A and B, so the tangent lines at A and B are Euclidean diameters of the circle. Thus the center is the intersection of these two tangents.
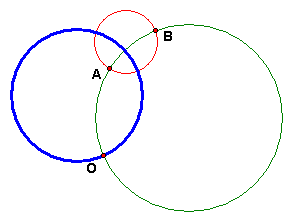
The relationship between the D-perpendicular bisector and the D-circle with D-diameter AB: Each pair of the 3 circles is orthogonal. The E-perpendicular bisector intersects D-line AB at the D-midpoint of AB, which is also the D-center of the D-circle with D-diameter AB.
Suppose that c and d are orthogonal circles. Explain, if true, why the inversion of d in c is d and the inversion of c in d is c.
AnswerTo explain why the inversion of d in c is d, we can either (a) use a theorem about inversion images of circles or (b) go back to the definitions and basic circle facts about secants. Either one is OK.
(a) By the theorem on inversion images of a circle, the inversion of d in c is a circle d'. If A and B are the intersection points of c and d, then A' = A and B' = B since the points are on c. Thus A and B are also the intersection points of d' and c. In addition, since angles are preserved by inversion, d' is orthogonal to c at A and B. But so is d. This shows the circles are the same. We see that they have the same center because of the orthogonality. The center of both d and d' is the intersection D of the tangents to c at A and B. So both circles have center D and pass through A. Thus d = d'.
(b) Let C be the center of c, and let c and d intersect in A and B. The the lines CA and CB are tangent lines to d, since the circles are orthogonal. Also CA = R, the radius of c. For any point P on d distinct from A and B, the line CP intersects d in a second point Q so that CP CQ = CA2 = R2. By definition, this means that Q is the inversion of P in c. Thus any point P on d inverts to another point Q on d. Since this is true for all points, it means that the inversion image of d is d.
The proof that the inversion of c in d is c is the same statement, with roles reversed. No additional proof needed.
Suppose c has center (0,0) and radius R. If circle d has equation x2 + y2 + Ax + By + C = 0, what is the equation of the inversion image of d?
Demonstrate that this is the equation of a circle (except in special cases – explain those cases).
First, you need a formula for the inversion of P = (x,y). This can be obtained from the definition and the parametric equation of a line.
Let d = |OP| = sqrt (x2 + y2 ). Then the inversion point P' is on the ray OP, so first of all it is a point of the form (1-t)O + tP = tP for some t > 0. Also R2 /d = |OP'| = |tP| = t |P| = td, so t = R2 /d2 .
Thus (x', y') = P' = (R2 /d2)P = (R2 /(x2 +y2 ))(x,y).
Also, since P'' = P, the formula gives (x,y) = (R2 /(x'2 +y'2 ))(x',y').
Now substitute in the equation for the circle:
x'2 + y'2 + Ax' + By' + C = ((R2 /d2))2 + ((R2 /d2))2 + A(R2 /d2) + B(R2 /d2) + C = 0
Thus (R4 /d4)(x2 + y2) + (R2 /d2)Ax+By) + C = (R2 /d2) + (R2 /d2)Ax+By) + C = 0.
since (x2 + y2) = d2.
Finally, using (x2 + y2) = d2 again,
0 = R4 + R2 (Ax+By) + Cd2 = R4 + R2 (Ax+By) + C(x2 + y2).
Notice that C = 0 exactly when the point O is a solution of the equation of the original circle. This is when the inversion of the circle is a line.