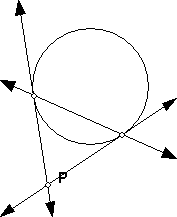
The Polar Line of a Point
- In this figure P' and Q' are inversions of P and Q, show that triangle PQ'O
is similar to QP'O.
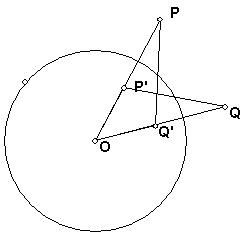
- The polar line (or just polar) of a point P with respect to a circle c that
has center O is the line orthogonal to OP that passes through the inversion
P'. In the figure below, prove that if Q is on the polar of P, then P is
on the polar of Q. (Hint: Use A.)

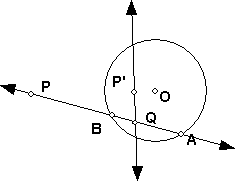
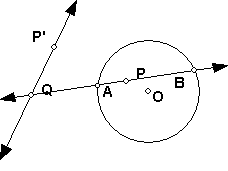
- Prove that if a secant intersects the polar of P at Q and intersects the
circle at A and B, then AB divides PQ harmonically. (Hint: Construct the
circle through P, P' and Q. Notice that as in one of the figures below, P
can be inside the circle.)
- Use what we know about the harmonic sets and the complete quadrilateral
to show that if two secants through P intersect the circle in A and B and
in C and D, then the polar of P is the line through the intersection of line
AC and line BD and the intersection of line AD with line BC. Does this construction
still work if P is inside the circle? Construct an example.
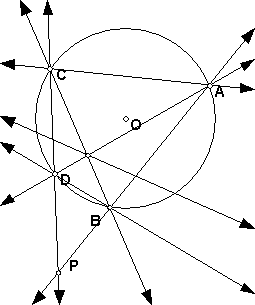
- Use D to explain how to construct the two tangent lines to the circle through
P only using a straightedge. The trick is that the points of tangency are
the intersection points of the polar of P with the circle (when P is outside
the circle).